Двойственная задача – это вспомогательная задача ЛП, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой задачи.

Прямая задача в исходной форме:

при ограничениях:

   .

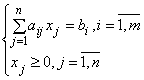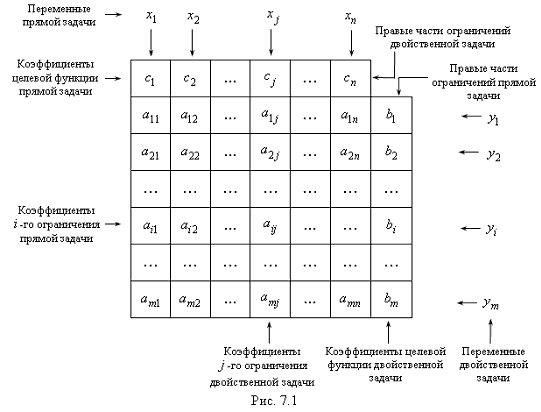Чтобы сформулировать условия двойственности задачи, составим следующую схему (рис. 7.1).

Из приведенной схемы видно, что двойственная задача получается путем симметричного структурного преобразования условий прямой задачи в соответствии с правилами:

1) каждому ограничению прямой задачи соответствует переменная двойственной задачи;

2) каждой переменной прямой задачи соответствует ограничение двойственной задачи;

1) коэффициенты при переменной (-й), фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи;

2) коэффициент при переменной в целевой функции прямой задачи, становится постоянной правой части соответствующего ограничения двойственной задачи;

3) постоянная правой части некоторого ограничения прямой задачи, становится соответствующим коэффициентом при переменной в целевой функции двойственной задачи;

4) если прямая задача решается на максимум целевой функции, то двойственная задача решается на минимум, и наоборот. Переменные двойственной задачи не ограничены в знаке;

5) если прямая задача решается на максимум, то ограничения в двойственной задаче имеют вид неравенства , если задача решается на минимум, то смысл неравенства противоположен.

Пример 7.1

Прямая задача:

,

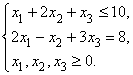
Стандартная форма прямой задачи:

,

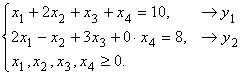
Двойственная задача:

                              

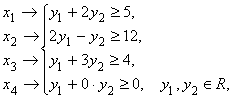
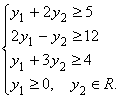
Из указанных правил следует: двойственная задача имеет  переменных (, , , ) и  ограничений (соответствующих  переменным прямой задачи , , , ).

Доказано, что для каждой пары двойственных задач справедливы свойства:

1) для любой пары допустимых решений прямой и двойственной задач:

2) На любой итерации процесса решения прямой задачи:

3) для оптимальных решений прямой и двойственной задач значения целевых функций совпадают, т.е.

,                                                     (7.1)

где звездочка (*)означает, что значения переменных берутся из оптимальных решений прямой и двойственной задач;

4) для каждой пары сопряженных условий в оптимальном решении выполняются следующие соотношения: если одно из них выполняется как простое равенство, то другое – как строгое неравенство и наоборот, т.е.

если , то ,                                             (7.2) 

если ,  то ,                                            (7.3)

если , то ,                                            (7.4)

если , то .                                            (7.5)

Опираясь на сформулированные свойства, можно дать следующую экономическую интерпретацию переменным двойственной задачи, которые в дальнейшем будем называть двойственными оценками.

1. Оценка ресурса показывает, на сколько изменится оптимальное значение целевой функции исходной задачи (суммарный объем выручки), если объем соответствующего ресурса изменить на единицу. Если же объем -го ресурса изменить на  единиц, то целевая функция изменится на величину  в случае, если это изменение не выйдет за границы устойчивости двойственных оценок.

2. Если ресурс в оптимальном плане израсходован полностью, то его оценка положительна (см. формулу (7.2)), если же ресурс не полностью израсходован в оптимальном плане, то его оценка равна нулю (см. формулу (7.3)). В первом случае ресурс является дефицитным, во втором – недефицитным. Для недефицитного ресурса значение соответствующей балансовой переменной покажет его остаток после выполнения оптимального плана. Чем больше оценка ресурса, тем он дефицитнее с точки зрения его вклада в поставленную цель – максимизировать суммарную выручку.

3. В оптимальный план включается производство только тех видов продукции, оценка ресурсов на производство единицы которых совпадает с ценой (см. формулу (7.5)) (такую продукцию будем называть рентабельной) и продукция не выпускается в оптимальном плане, если аналогичная оценка превышает цену (см. формулу (7.4)).

Проиллюстрируем рассмотренные положения на следующем примере.

Пример 7.2

Пусть в производстве 4-х видов продукции используется 4 вида ресурсов. Известны нормы расхода ресурсов на производство единицы продукции, цены ее реализации

и запасы ресурсов. Определить план производства продукции, максимизирующий выручку от реализации произведенной продукции.

Пусть  – матрица коэффициентов расхода ресурсов на производство единицы каждого вида продукции,  – матрица-столбец объемов ресурсов,  – матрица-строка цен реализации единицы продукции, причем для рассматриваемой задачи они следующие:

;  ;  .

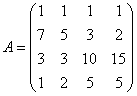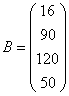Решение. Модель задачи примет вид:

Найти , ,  и  (объемы производства каждого вида продукции), удовлетворяющие ограничениям:

,

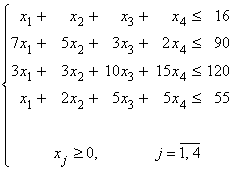при которых функция  достигает максимума.

Для решения задачи симплексным методом приведем ее к стандартному виду:

.

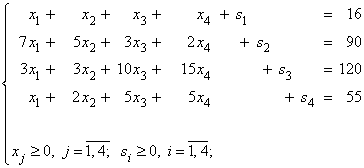
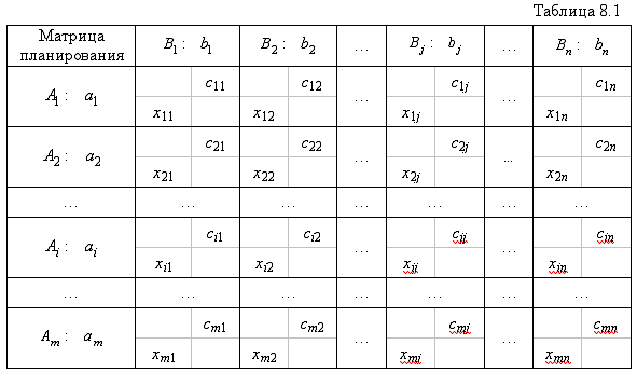
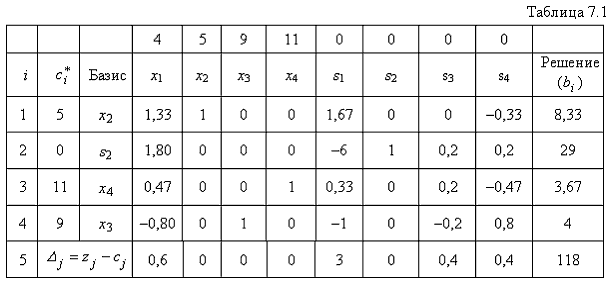
Значения балансовых переменных показывают объемы неизрасходованных ресурсов в соответствующем плане. Последняя симплексная таблица при решении этой задачи имеет вид табл. 7.1.

Итак, для получения максимального дохода от реализации произведенной продукции необходимо выпустить ее в объемах:

; ; ; .

При этом .  – это остаток неизрасходованного второго ресурса.

В таблице 7.1 оптимального решения имеется также вся информация о решении двойственной задачи. Как известно, это – оценки балансовых переменных. Выпишем сначала двойственную задачу, а затем и ее решение.

Двойственная задача.

Найти значения переменных , удовлетворяющих ограничениям

,

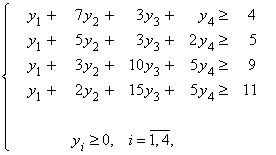для которых целевая функция достигает минимума. Решение этой задачи выпишем из последней строки таблицы (с противоположным знаком):

; ; ; . .

При этом оптимальные значения целевых функций получились одинаковыми (см. формулу (7.1)).

Проиллюстрируем свойства двойственных оценок на основе этой задачи.

1. Каждая из оценок указывает, на сколько изменится максимальное значение целевой функции (максимальная выручка), если изменить на единицу запасы соответствующих ресурсов. Как видим, наибольшее изменение выручки произойдет, если изменить объем первого ресурса , а изменение второго ресурса не приведет к изменению целевой функции. По крайней мере, его увеличение не приведет к увеличению выручки, так как (как мы видим) этот ресурс остался в излишке в оптимальном решении, но если мы его изменим до величины, меньшей 61 , то выручка уменьшится. Проверьте самостоятельно, что, подставив оптимальное решение во второе ограничение исходной задачи, получим, что для выполнения этого плана второго ресурса понадобится как раз 61 ед., а 1-й, 3-й и 4-й ресурсы израсходованы полностью.

2. Наиболее дефицитным является 1-й ресурс, так как его оценка наибольшая, недефицитным – 2-й (его оценка равна нулю), в 3-й и 4-й ресурсы по дефицитности равнозначны (их оценки равны).

3. Рентабельными являются 2-я, 3-я и 4-я продукции (эти виды продукции выпускаются), а нерентабельной – 1-я . Подставив в первое ограничение двойствен-

ной задачи оценки оптимального плана, получим, что оценка ресурсов, необходимых для выпуска единицы первого вида продукции, равна:

,

что на 0,6 больше цены единицы этой продукции, равной 4 (обратите внимание, что число 0,6 находится в оценочной строке столбца «x₁» в таблице 7.1).