Постановка задачи. Имеется m – станков (m – групп станков), на которых могут быть изготовлены n – типов деталей. Трудоемкость обработки j — ой детали на i – м станке составляет , час. Известны фонды времени работы каждого станка (группы станков) – B_i. Исходные данные для решения задачи представлены в таблице 8.1.

Таблица 8.1. Исходные данные для решения задачи, представленные в общем виде

Требуется определить количество деталей каждого наименования , при обработке которых достигается максимальная загрузка оборудования участка.

Математическая модель для решения задачи запишется:

Ограничения:

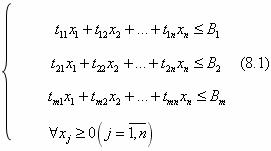
Управляемые параметры:

.

Целевая функция:

Задача решается методом линейного программирования (глава 7). При этом следует иметь в виду следующее. Количество ограничений вида (8.1) в математической модели должно строго равняться количеству станков (групп станков) участка. При решении задачи с помощью компьютера количество станков (групп станков), а также типов деталей практически не ограничено и определяется только возможностями компьютера и соответствующей программы. При решении задачи вручную с применением графо-аналитического метода количество типов станков (групп станков) также не ограничено, но их увеличение естественным образом приведет к увеличению времени расчетов. Количество же типов деталей не должно превышать двух, т.к. в противном случае невозможно будет на плоскости выполнить необходимые графические построения.

Пример 1. Исходные данные для примера приведены в таблице 8.2.

Таблица 8.2. Исходные данные для решения задачи

Обозначим через  количество деталей типа D₁, через  количество деталей типа D₂.

Математическая модель для решения данной задачи запишется следующим образом:

Ограничения (по фонду времени работы оборудования):

Целевая функция (суммарное время работы всех групп оборудования):

   (8.3)

Требуется найти значения  и , удовлетворяющие заданным ограничениям (8.2) и обеспечивающие максимум целевой функции (8.3). Параметры  и  являются управляемыми параметрами в математической модели.

Решим задачу графо – аналитическим методом (см. раздел 7.2.1.). Графическая иллюстрация решения задачи приведена на рис. 8.1.

Вычисления для построения ограничений (8.2):

Направления допустимости первых трех ограничений (8.2) – «вниз – влево».

Последние два ограничения в системе (8.2) – это оси координат. Направления их допустимости – «вправо» и «вверх».

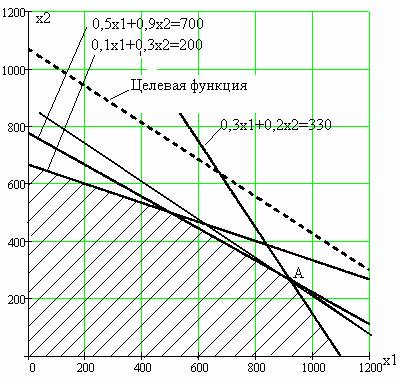
Рис.8.1 Графическая иллюстрация решения задачи

Для нахождения точки касания границы ОДР прямой линией, определяющей целевую функцию, построим сначала произвольную прямую для целевой функции, приравняв ее выражение к произвольному числу в пределах масштаба построений, например к 1500:

Проведя прямую линию, параллельную данной, находим точку касания ее границы ОДР – это точка А. Для нахождения ее координат решаем следующую систему уравнений:

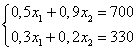
т.е. окончательно шт., шт.

Максимальное значение целевой функции (максимальная загрузка оборудования участка) при оптимальных значениях искомых параметров составит:

 час

Пример решения задачи в MathCAD представлен на рисунке 8.2.

Рис. 8.2 Решение задачи в MathCAD