Эта задача относится к задаче производства одного или нескольких взаимозаменяемых видов продукции, но в условиях, когда наличные мощности поставщиков не достаточны для удовлетворения спроса потребителей. Это требует ввода новых мощностей за счет капитального строительства и реконструкции.

Обычно существует несколько возможных вариантов строительства и реконструкции, отличающихся по производственной мощности, местоположению, уровню капитальных затрат и другим показателям.

К задаче оптимального закрепления потребителей за поставщиками добавляется задача оптимального прироста мощности. Решение данной задачи должно обеспечить определение оптимальных вариантов размещения производства и перевозок продукции, при которых достигается минимум суммарных текущих затрат на производство продукции, ее транспортировку и приведенных капитальных вложений (оптимальных инвестиционных вложений) в создание новых мощностей или расширение действующих.

Математическая модель задачи:

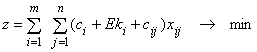
при ограничениях:

,

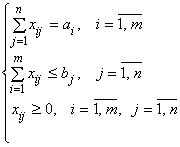где        – затраты на производство единицы продукции на действующем предприятии;  – нормативный коэффициент эффективности капитальных вложений;  – капитальные удельные вложения в i-ое предприятие;  – искомый объем перевозок продукции i-го поставщика j-му потребителю;  – мощность i-го предприятия-поставщика;  – спрос j-го потребителя;

Эта модель представляет собой открытую транспортную задачу, которая приводится к закрытой введением условного потребителя. Поставщиков, которые в оптимальном плане «прикрепились» к условному потребителю, использовать нецелесообразно. Если это относится к проектируемому предприятию, то соответствующий вариант отбрасывается, как нерациональный.

Если же к условному потребителю «прикрепилось» какое-либо действующее предприятие, то следует рассмотреть вопрос о целесообразности его дальнейшей эксплуатации. Как правило, в оптимальный план попадают действующие предприятия.

Приведенные затраты на единицу продукции на этих предприятиях ниже, чем на проектируемых. Здесь к затратам на производство продукции добавляются капитальные затраты.

Основная трудность при решении такого рода задач заключается в возможности получения нецелочисленных решений, когда в оптимальном плане часть мощности какого-либо поставщика относится на действительных, а часть – на условных потребителей. В таких случаях приходится останавливаться на приближенных решениях.

Пример 9.4

Два действующих предприятия  и  имеют дневную производительность 240 и 360 единиц продукции. Предприятия обеспечивают трех потребителей с потребностями 220, 280 и 200 единиц продукции. Недостающий прирост мощности планируется за счет реконструкции первого предприятия  и (или) строительства нового предприятия . Себестоимость единицы продукции на действующих предприятиях 3,5 и 3 тыс. руб., после реконструкции действующего предприятия – 3 тыс. руб., в результате строительства нового предприятия – 2,5 тыс. руб. Удельные капитальные затраты на реконструкцию – 2 тыс. руб., а на строительство – 3,5 тыс. руб. Матрица транспортных затрат за доставку единицы продукции известна:

.

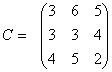Определить оптимальный план перевозок и прироста мощностей.

Решение.  ,   .

Каждому проектируемому варианту прироста мощности выделяем отдельную строку и даем недостающую мощность 100 ед. Затраты для действующих предприятий складываются из затрат на производство единицы продукции и транспортировку ; для вариантов реконструкции и строительства учитываются еще удельные капитальные затраты: . Первоначальный опорный план  составляем по методу минимальной стоимости. Последовательность заполнения клеток:  (2, 2);  (2, 1);  (1, 1);  (4, 3);  (1, 3);  (3, 3); (3, 4) (табл. 9.6).

Таблица 9.6

Вычисляем стоимость этого плана:

.

Задачу решаем методом потенциалов. Последовательность определения потенциалов:     .

Последовательность определения оценок незанятых клеток:

.

План  не является оптимальным, так как содержит положительную оценку , строим для нее цикл: (2, 3) – (2, 1) – (1, 1) – (1, 3) – (2, 3).

Свободную клетку помечаем знаком + и далее чередуем знаки по вершинам контура. Величина перемещаемой поставки равна  .

После перераспределения объемов поставок по контуру, получим новый план (табл. 9.7), при этом целевая функция уменьшится на величину: . Этот план является оптимальным (проверьте).

Таблица 9.7

Из таблицы 9.7 оптимального плана получаем, что оптимальным вариантом прироста мощности является вариант строительства нового предприятия, так как вариант реконструкции приходится на «фиктивного» потребителя.

Полученное оптимальное решение является целочисленным, т.е. все мощности предприятий не дробятся между реальными и фиктивными потребителями.