Обычно вопрос нахождения функции по полному дифференциалу рассматривают в разделе функций нескольких переменных. Поскольку эта операция играет важную роль в приложениях, то, не прибегая к строгости построения такой функции, покажем на примерах этот процесс.

Пример 1

Вычислить:

Решение. Здесь Х = y², Y = 2xy, поэтому проверяем условие (1.30) (которое называют часто условием интегрируемости по формуле Ньютона-Лейбница (1.28)).

Видно, что условие интегрируемости выполняется. Найдем неопределенный интеграл:

.

Имеем:

Подберем функцию  так, чтобы , т.е. чтобы , откуда , тогда .

Итак,

,

то есть

.

Берем из этого неопределенного интеграла первообразную (частную при с = 0) .

По формуле Ньютона-Лейбница (1.28) находим:

.

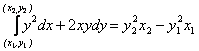Например, при  и  получим

Пример 2

Вычислить: .

Решение. Условие интегрируемости (1.30) выполняется (проверьте). Найдем:

.

Имеем:

.

Подберем  так, чтобы , т.е. чтобы , откуда

, тогда  ,

то есть

.

Тогда (с = 0)

.

Задачи для упражнений

1) Вычислить следующие криволинейные интегралы, независящие от пути интегрирования:

а) ,                                                           Ответ: -2.

б) ,  (у >0)                                             Ответ: 0.

в) ,                                                           Ответ: .

г) ,                                                     Ответ: .

2) Вычислить работу, производимую вдоль окружности  переменной силой  . Почему здесь работа равна нулю?