Предложенное изложение интегрального исчисления функций нескольких переменных отличается от обычного тем, что одновременно вводятся все типы интегралов (двойные, тройные, поверхностные), за исключением поверхностных и криволинейных интегралов второго рода. Такое изложение [1] имеет преимущества в подготовке специалистов и более экономно, компактно, просто, наглядно и удобно для преподавания таких дисциплин как теоретическая механика, физика и сопротивление материалов.

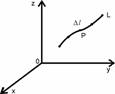
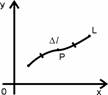
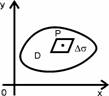
Будем называть фигурой либо линию, либо поверхность, либо пространственное тело (рис. 1.4). Диаметром фигуры будем называть максимальное из расстояний между двумя её точками. Например, для эллипса диаметр равен  его диагонали; для шара и круга диаметру в обычном смысле. Имеем дело с ограниченными фигурами.

        а)                                             б)                                          в)

      г)                                                д)                                           е)

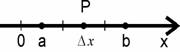
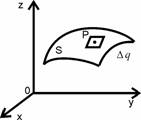
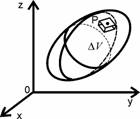
Рис. 1.4

Каждой фигуре присуща её мера. В случае линий под мерой понимаем их длину; в случае поверхностей – их площадь; в случае пространственных тел мерой будет служить объём.

Рассматривая фигуру, мы будем мыслить её материальной, т.е. имеющей определенную массу. С массой фигуры связано понятие плотности. Обычное определение плотности – количество массы в единице объема. В случае стержня (отрезка) говорят о линейной плотности; в случае пластины – поверхностной плотности.

Рассмотрим произвольную точку  (см. рис. 1.4,а) и содержащий эту точку отрезок . Массу отрезка  обозначим . Тогда плотность равна:

.                                                            (1.32)

Аналогично определяется плотность и для других фигур. В каждой точке любой из рассмотренных фигур плотность, вообще говоря, своя. Поэтому плотность  – является функцией точки Р:

1) для отрезка ;

2) для плоской области

3) для пространственных фигур