В полярных координатах можно вычислить важный для теории вероятностей и уравнений математической физики интеграл Эйлера-Пуассона:
![]() . (1.58)
. (1.58)
Так как интеграл не зависит от обозначения переменной интегрирования, то записывается также:
![]() (1.59)
(1.59)
Умножая почленно последние равенства, придем к двойному интегралу:
![]() , (1.60)
, (1.60)
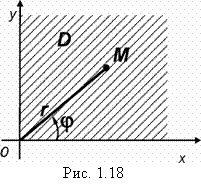
где D: ![]() (рис. 1.18).
(рис. 1.18).
В полярных координатах:
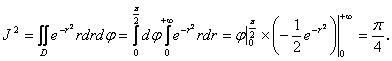
Отсюда, учитывая, что J > 0, находим:
![]()
В силу четности функции ![]() , получим:
, получим:
![]()
что представляет собой площадь, ограниченную осью Ох и кривой Гаусса ![]() .
.
Задачи для упражнений
1) Вычислить интегралы:
а) ![]() ; Ответ:
; Ответ: ![]() .
.
б) ![]() ; Ответ:
; Ответ: ![]() .
.
в) ![]() ; Ответ:
; Ответ: ![]() .
.
2) Изменить порядок интегрирования:
а) ![]() ; Ответ:
; Ответ: 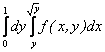 .
.
б) ![]() ; Ответ:
; Ответ: ![]() .
.
в) ![]() . Ответ:
. Ответ: ![]() .
.
3) Перейти к полярным координатам и расставить пределы интегрирования:
а) ![]() , где D – круговой сектор, ограниченный линиями:
, где D – круговой сектор, ограниченный линиями:
![]() Ответ:
Ответ:  .
.
б) ![]() , где D – треугольник с вершинами O(0,0), A(2,-1) и B(2,1);
, где D – треугольник с вершинами O(0,0), A(2,-1) и B(2,1);
Ответ: ![]() .
.
4) Найти объемы тел, ограниченных поверхностями:
а) ![]() Ответ:
Ответ: ![]() .
.
б). ![]() . Ответ:
. Ответ: ![]() .
.
в). ![]() Ответ:
Ответ: ![]() .
.