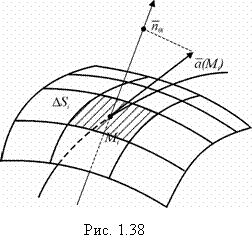
Пусть задано векторное поле 
– вектор скорости несжимаемой жидкости, которая движется стационарно. Как отмечено выше, векторные линии будут линиями тока жидкости. Пусть в потоке находится поверхность S. Подсчитаем количество жидкости, протекающей через поверхность за единицу времени. Для этого применим известный в интегральном исчислении метод: разобьем поверхность S на n элементарных площадок: 
; в каждой 
выберем произвольно точку и построим в ней нормаль 
(если S – замкнутая, то нормаль берем внешнюю).
Площадку 
будем считать плоской в виду её малости, а вектор 
постоянным во всех точках (рис. 1.38).
Тогда количество жидкости 
, протекающей через площадку , будет:
, (1.96)
где 
. Представим площадку в виде вектора: 
, тогда
. (1.97)
Общее количество жидкости П получим, просуммировав потоки 
(i = 1, 2,…, n):
. 1.98)
Точное значение количества жидкости П найдём, перейдя к пределу в выражении (1.98):
. (1.99)
Таким образом, количество жидкости, протёкшей через S в единицу времени, будет равняться объёму жидкости, прошедшей через S. Этим объясняется выбор названия «поток».
Исходя из (1.99) можно дать определение потока: потоком П векторного поля 
через поверхность S (в выбранном направлении нормалей к S), расположенную в области Д, называется поверхностный интеграл второго рода:
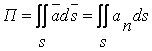(1.100)
Другими словами, величина интеграла в (1.100) называется потоком вектора через поверхность S.
Вычислим величину П. Так как
,
,
то
. (1.101)
Замечание 1. В электротехнике понятие потока вектора имеет особо важное значение. Например, поток вектора плотности тока 
сквозь некоторую поверхность S представляет собой ток i, проходящий через эту поверхность:
.
Из этого равенства видно, что электрический ток есть величина скалярная; это и учитывается при расчете электрических сетей.
Замечание 2. Аналогично магнитный поток 
представляет собой поток вектора магнитной индукции 
через поверхность S;
,
где 
- вектор магнитной индукции; 
- абсолютная магнитная проницаемость среды; 
- вектор напряженности магнитного поля.
Замечание 3. Особый интерес имеет случай, когда S – замкнутая поверхность и ограничивает некоторый объём V. Тогда поток записывается так:
. (1.102)
Говорят, что поток вектора через замкнутую поверхность представляет собой разность между числом векторных линий, выходящих и входящих в объем, ограниченный этой поверхностью.
Используя связь поверхностного интеграла с тройным (1.88), получим:
, (1.103)
где величину
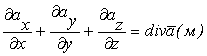(1.104)
обозначают 
и называют дивергенцией (расходимостью) векторного поля 
. Отметим, что дивергенция векторного поля – величина скалярная и является одной из характеристик теории поля.
Вывод: поток равен тройному интегралу от дивергенции векторного поля (нормаль Вещиля).
Методическое руководство
1) При вычислении потока используют формулу (1.100) и тогда говорят, что мы применяем метод непосредственного вычисления потока.
2) Когда поверхность S – замкнутая, то пользуются формулой Остроградского (1.103).
3) Формулу Остроградского можно применить и тогда, когда поверхность S – не замкнутая, но тогда надо дополнить заданную поверхность S до замкнутой некоторой поверхностью S1 (желательно простой). Получим:
. (1.105)
Интересующий нас поток через S тогда будет:
.
При этом 
– находят по формуле Остроградского, а 
– обычным способом.
Пример 1
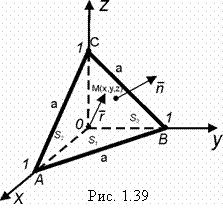
Найти поток радиуса-вектора 
через плоскость 
, заключённую в первом октанте; нормаль внешняя (рис. 1.39).
Решение
Способ 1
Дано: 
, нормаль к поверхности: 
запишется так: 
. Тогда по определению потока
на поверхности S 
, поэтому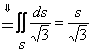 
.
Найдем S. Для этого вычислим площадь равностороннего треугольника ABC со стороной 
: 
.
Тогда
.
Способ 2
Дополним поверхность S до замкнутой полной поверхности пирамиды, треугольниками 
, 
, 
, лежащими в координатных плоскостях. Тогда по формуле Остроградского:
,
;
.
.
Тогда
.
Пример 2
Найти 
, если 
Решение. Имеем: 
; 
; 
, тогда по (1.104)
; 
; 
; 
.
Инвариантное определение дивергенции. По теореме Остроградского
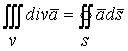
По теореме о среднем значении имеем:
,
где 
– некоторая точка объема V. Найдя предел, получим:
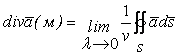
Определение. Дивергенцией векторного поля в точке М называется предел отношения потока поля через малую замкнутую поверхность, окружающую точку М, к объёму тела, ограниченного этой поверхностью, при стремлении диаметра к нулю. Эти рассуждения показывают, что любое поле 
порождает скалярное поле дивергенции 
.
Векторное поле называется солиноидальным (или трубчатым) в области D, если S – любая замкнутая поверхность, где поле существует везде.
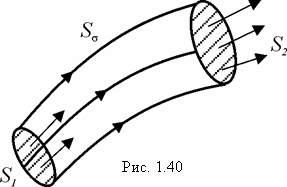
Рассмотрим векторную трубку (рис. 1.40), где 
и 
- два произвольных сечения, тогда
(нормаль внешняя).
Если на боковой поверхности 
, то:
и 
.
Это говорит о том, что поток через сечение такой же, как через 
, т.е. потоки имеют одно и тоже значение. Это значение называют интенсивностью векторной трубки.
Из формулы Остроградского следует связь между потоком и дивергенцией, так:
1) если 
, то 
- говорят, что в точке М есть сток;
2) если 
, то 
- говорят, что в точке М есть источник;
3) если 
– отсутствует сток или источник (речь идет о бесконечно малом объеме точки М).
Абсолютная величена 
– характеризует мощность источника или стока.