Английский математик и механик Гамильтон показал, что операции нахождения , ,  можно записать проще, если ввести в рассмотрение оператор «набла» (далее его называют оператором Гамильтона):

.

Этот оператор по своей природе векторно-дифференциальный [7]: при его применении он сохраняет свойства вектора и свойства оператора. Так

1)           ;

2)           ;

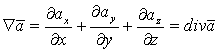3)          

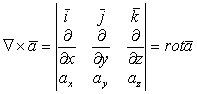
Так, первое уравнение Максвелла будет иметь вид:

.

Если в выражении за оператором нет множителей, то это выражение есть новый оператор:

т.е. — это скалярный дифференциальный оператор. Например:

.

Мы рассмотрели некоторые дифференциальные операции первого порядка (назвали потому, что участвуют в нахождении понятий операции дифференцирования первого порядка). После их применения к полю получается новое поле (солярное или векторное), к которому, в свою очередь, как изначальному можно еще раз их применить. В результате, приходим к операциям второго порядка. Надо следить, чтобы операции имели смысл. Так, если записать , то это не имеет смысла, так как дивергенция берется от вектора, а у нас - скаляр. Другая запись:  — может быть, ибо градиент – находят от скалярной функции и прочее.

Имеется лишь пять операций второго порядка:

1) ;  здесь 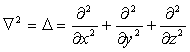 – есть оператор Лапласа.

2) ;

3) ;

4)  (поле вихря соленоидально);

5) .