Функция, имеющая производную в точке z, называется дифференцируемой в этой точке. Рассмотрим условия дифференцируемости функции

.

Теорема. Пусть функция  определена в некоторой окрестности точки , причем в этой точке функции  и  дифференцируемы. Тогда для дифференцируемости функции  необходимо и достаточно, чтобы в этой точке имели место условия:

.                                                   (2.31)

Эти условия называются условиями Д’ Аламбера-Эйлера или Коши-Римана – условия дифференцируемости функции .

Доказательство. Докажем необходимость условий (2.31). Пусть  дифференцируемая в точке z; тогда функция имеет в  точке z производную. Следовательно, существует

и этот предел не зависит от закона стремления . А при , т.е. точки  к точке z по прямой параллельно оси Ох (рис. 2.12), получим:

а)                                                              б)

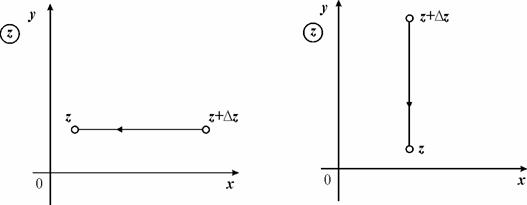
Рис. 2.12

.                   (2.32)

Если идти по пути прямой, параллельной мнимой оси от  (, х – фиксировано, а ) (рис. 2.12 б), получим:

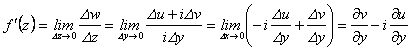.                 (2.33)

Так как предел единственный, а функция  однозначная, то (2.32) и (2.33) дают:

.

Достаточность имеет место. Приведем схему доказательства этого. Дано, что  и  – дифференцируемые, т.е. имеют полные дифференциалы, а значит, имеют место условия дифференцируемости функций двух независимых переменных

,                                      (2.34)

,

где  при  для  имеем:

.                                                         (2.35)

Подставляя значения  и  из (2.34) в (2.35) и, заменяя  равными им значениями частных производных по переменной х, исходя из условий (2.31), в пределе получим:

.

Тем самым достаточность условий (2.31) доказана.

Вывод: производную от функции  при выполнении условий (2.31) можно находить по одной из формул (2.32) или (2.33), не прибегая к таблице производных.

Например, для  по таблице производных  . С другой стороны:

.

Проверяем условия (2.31.):  – условия дифференцируемости выполнены для любого z. Применяя формулу (2.32), получим:

.

Если однозначная функция дифференцируема не только в точке, но и в некоторой окрестности ее, то она называется аналитической в данной точке.

Функция, дифференцируемая во всех точках некоторой области, называется аналитической в этой  области (регулярной) или голоморфной (т.е. имеющая форму целой функции). Поэтому ТФКП часто называется теорией аналитических функций.

Точки плоскости z, в которых  является аналитической – называются   правильными точками однозначной функции, а те, в которых f(z) не является аналитической – называется особыми точками (и в частности, в которых  не определена). Условия (2.31) являются условиями аналитичности функции в области.

Пример 1

Выяснить, является ли  аналитической.

Решение. Решая предыдущий пример мы проверили условия (2.31) и убедились, что они имеют место для любого z плоскости хОу. Следовательно, функция является аналитической (регулярной) во всей плоскости.

Пример 2

Выяснить, является ли регулярной функция .

Решение. , то , отсюда  – условия (2.31) не выполняются нигде в плоскости z. Значит,  не дифференцируема ни в одной точке плоскости.

Пример 3

Выяснить, является ли аналитической функция .

Решение. Найдем связь u и v с х и у:

 и  ;

.

Условие (2.31) выполнено только для х = 0 и у = 0. Следовательно,  дифференцируема только в одной точке  и нигде не является аналитической.

Пример 4

Выяснить, является ли аналитической функция .

Решение. .

.

Условия (2.31) выполняются только в точке х = 0, у = 0, т.е.  – единственная точка, где функция дифференцируемая и нигде не является регулярной.

Пример 5

Используя условия (2.31), доказать аналитичность функции  на всей плоскости, получить формулу .

Решение. .

Ясно, что эти функции дифференцируемы при всех х и у. Условия (2.31):  – выполняются. Следовательно,  дифференцируемая в любой точке z, т.е. аналитическая на всей комплексной плоскости. По формуле (2.32):

.