Пусть функция w = f(z) – аналитическая в окрестности точки z₀, за исключением самой точки (т.е. z₀ – изолированная особая точка функции w = f(z)).

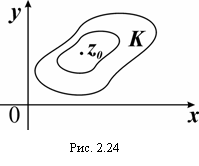
Пусть К – замкнутый контур, лежащий в указанной окрестности и содержащий z₀ (рис .2.24).

Определение. Вычетом функции w = f(z) относительно z₀ называется выражение:

.                                                         (2.83)

Вычет обозначается:  или res f(z₀)  (происходит от слова resudi – остаток):

.                    (2.84)

Теорема: Вычет относительно устранимой особой точки равен нулю.

Доказательство: Пусть z₀ – устранимая точка, тогда функция

будет аналитическая в окрестности z₀ и по теореме Коши  что и требовалось доказать.

Теорема Коши о вычетах: если функция w = f(z)  аналитическая в конечной замкнутой области , ограниченной контуром К, за исключением конечного числа особых точек z₁, z₂,…,z_n , лежащих внутри , то

.                (2.85)

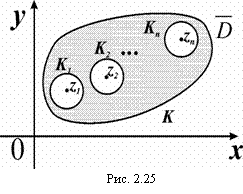
Доказательство: Опишем из каждой особой точки z_К  (k = 1, 2,…,n) как из центра, окружности К_к настолько малого радиуса, чтобы они целиком лежали в  и не содержали других особых точек функции f(z) (рис. 2.25).

В многосвязной области f(z) будет аналитической. По теореме Коши:

.

Умножим и разделим правую часть последнего равенства на 2p I получим:

.                               (2.86)

Что и требовалось доказать.

Найдем вычет относительно простого полюса. Пусть f(z) имеет в точке  простой полюс, тогда

.

Следовательно, для функции (z-z₀) f(z) точка z₀ – устранимая. Рассмотрим функцию

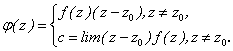
Как отмечено ранее она аналитическая в окрестности  z₀ и по формуле Коши

.

Но на контуре К:, поэтому

.

Вывод: вычет относительно простого полюса находят по формуле:

.                                             (2.87)

Пример 1

Найти вычет функции  относительно точки z = 0.

Решение. Для функции  точка z = 0 – простой полюс. Поэтому

Методическое руководство

Если функция , где ,  – аналитические в точке z₀, причем для  точка z₀  есть нуль первого порядка, а , то для вычисления вычета относительно простого полюса можно пользоваться формулой:

,                                                          (2.88)

Формула (2.88) получается сразу:

Пример 2

Найти вычет w = ctg z относительно z = 0.

Решение. Согласно формуле (2.88)

так как z = 0 – простой полюс.

Пример 3

Вычислить .

Решение. Функция имеет две особые точки z = 0  и  z = 2;  обе точки попадают в область, ограниченную окружностью |z| = 3. Точка  z = 0 – устранимая, так как

,

а вторая – простой полюс (сделайте рисунок).

Вычет относительно устраненной точки равен нулю. Вычет относительно точки z = 2 находим по формуле (2.88):

.

По основной теореме Коши о вычетах (2.85), получим:

.

Вывод формулы для нахождения вычета относительно кратного полюса аналогичен рассуждениям, проведенным для случая простого полюса, а именно: если f(z) имеет в точке z₀ кратный полюс, то для функции  (k – кратность полюса) точка z₀ устранимая. Тогда функция

 

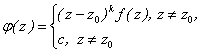
аналитическая в окрестностях z₀. Значит,

.

Но на контуре  поэтому

Вывод: получена формула для нахождения вычета функции относительно полюса порядка k:

.                                 (2.89)

Пример 4

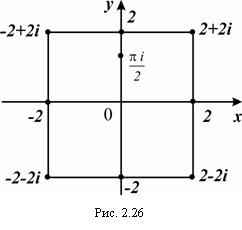
Вычислить 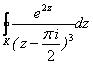, вдоль замкнутого контура К, соединяющего точки: 2+2i, -2+i,   -2-2i,   2-2i   и   2+2i  отрезками прямых (рис. 2.26)

Решение. Точка  – полюс третьего порядка функции 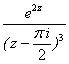. По формуле (2.89) имеем:

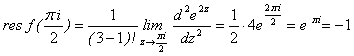
Следовательно,

.

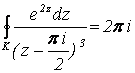Задачи для упражнений

Вычислить интегралы, используя основную теорему Коши о вычетах:

а) ;	б) ;
в) ;	г) ;
д) ;	е) ;
ж) ;	з) ;
и) ;	к) .

.

Ответы:

а) 0;	б) ;
в) ;	г) ;
д) ;	е) ;
ж) ;	з) ;
и) ;	к) .
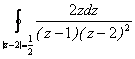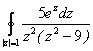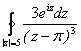