1. Пусть известен отрезок [a, b], который содержит один корень уравнения f(x) = 0. Функция f является непрерывно дифференцируемой функцией на этом отрезке (f(x)ÎC1[a, b]). При выполнении этих условий можно применять метод простой итерации.
2. По функции f(x) строится функция j(x), удовлетворяющая трём условиям: она должна быть непрерывно дифференцируемой (j(x)ÎC1[a, b]), такая, что уравнение x = j(x) равносильно уравнению f(x)=0; должна также переводить отрезок [a, b] в себя.
Будем говорить, что функция j(x) переводит отрезок [a, b] в себя, если для любого x Î[a, b], y = j(x) также принадлежит [a, b] (y Î [a, b]).
На функцию j(x) накладывается третье условие:
.
Формула метода: xn+1 = j(xn).
3. При выполнении этих трех условий для любого начального приближения x0Î[a, b] последовательность итераций xn+1 = j(xn) сходится к корню уравнения: x = j(x) на отрезке [a, b] (
).
Как правило, в качестве x0 выбирается один из концов [a, b].
4. Условие остановки итерационного процесса:
,
где e – заданная точность
Число xn+1 при выполнении условия остановки итерационного процесса является приближенным значением корня уравнения f(x) = 0 на отрезке [a, b], найденным методом простой итерации с точностью e.
Пример
Построить алгоритм для уточнения корня уравнения: x3 + 5x – 1 = 0 на отрезке [0, 1] методом простой итерации с точностью e.
Решение
1. Функция f(x) = x3+5x-1 является непрерывно дифференцируемой на отрезке [0,1], содержащем один корень уравнения.
2. Наибольшую трудность в методе простой итерации представляет построение функции j(x), удовлетворяющей всем условиям:
.
Рассмотрим: 
.
Уравнение x = j1(x) эквивалентно уравнению f(x) = 0, но функция j1(x) не является непрерывно дифференцируемой на отрезке [0, 1].
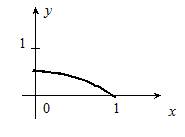
Рис. 2.4. График функции j2(x)
С другой стороны, 
, следовательно, 
. Отсюда: 
– непрерывно дифференцируемая функция. Отметим, что уравнение:x = j2(x) эквивалентно уравнению f(x) = 0. Из графика (рис. 2.4) видно, что функция j2(x) переводит отрезок [0, 1] в себя.
Условие, что функция j(x) переводит отрезок [a, b] в себя, можно переформулировать следующим образом: пусть [a, b] – область определения функции j(x), а [c, d] – область изменения j(x). Если отрезок [c, d] принадлежит отрезку [a, b], то функция j(x) переводит отрезок [a, b] в себя.
Найдем 
:
, 
.
Все условия для функции j(x) выполнены.
Формула итерационного процесса: xn+1 = j2(xn).
3. Начальное приближение: x0 = 0.
4. Условие остановки итерационного процесса:
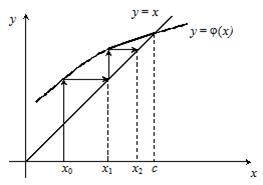
Рис. 2.5. Геометрический смысл метода простой итерации
.
При выполнении этого условия xn+1 – приближенное значение корня на отрезке [0,1], найденное методом простой итерации с точностью e. На рис. 2.5. иллюстрируется применение метода простой итерации.
Теорема о сходимости и оценка погрешности
Пусть отрезок [a, b] содержит один корень уравнения x = j(x), функция j(x) является непрерывно дифференцируемой на отрезке [a, b], переводит отрезок [a, b] в себя, и выполнено условие:
.
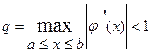Тогда для любого начального приближения x0Î[a, b] последовательность 
сходится к корню уравнения y = j(x) на отрезке [a, b] и справедлива оценка погрешности:
.
Устойчивость метода простой итерации. При выполнении условий теоремы о сходимости алгоритм метода простой итерации является устойчивым.
Сложность метода простой итерации. Объем памяти ЭВМ, необходимый для реализации метода простой итерации, незначителен. На каждом шаге нужно хранить xn, xn+1, q и e.
Оценим число арифметических действий, необходимых для реализации метода простой итерации. Запишем оценку для числа n0 = n0(e) такого что, для всех n ³ n0 выполняется неравенство: 
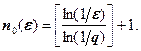
Из этой оценки вытекает, что чем ближе q к единице, тем медленнее сходится метод.
Замечание. Не существует общего правила построения j(x) по f(x) так, чтобы выполнялись все условия теоремы о сходимости. Часто используется следующий подход: в качестве функции j выбирается функция j(x) = x + k× f(x), где k – константа.
При программировании метода простой итерации для остановки итерационного процесса часто требуют одновременного выполнения двух условий:
и 
.
Все остальные итерационные методы, которые мы будем рассматривать, являются частными случаями метода простой итерации. Например, при 
метод Ньютона является частным случаем метода простой итерации.