Среди множества рядов, близких к степенным по своему строению и свойствам, являются ряды, расположенные по целым отрицательным степеням z – z0:
![]() 2.103)
2.103)
Сделаем замену 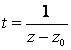 в (2.103), получим:
в (2.103), получим:
![]() . (2.104)
. (2.104)
Как известно радиус сходимости полученного ряда есть число R (2.90): если R = 0, то ряд (2.104) сходится в точке t = 0; если 0 < R < ¥ , то ряд сходится абсолютно в круге ![]() и расходится вне его; если R = ¥, то ряд абсолютно сходится в любой конечной точке плоскости. В виду замены
и расходится вне его; если R = ¥, то ряд абсолютно сходится в любой конечной точке плоскости. В виду замены  следует, что если
следует, что если ![]() , то ряд (2.103) расходится в каждой конечной точке; если
, то ряд (2.103) расходится в каждой конечной точке; если ![]() , то он абсолютно сходится при
, то он абсолютно сходится при ![]() и расходится при
и расходится при ![]() ; если
; если ![]() , то ряд абсолютно сходится во всех точках плоскости, за исключением z = z0. Если считать, что
, то ряд абсолютно сходится во всех точках плоскости, за исключением z = z0. Если считать, что ![]() ; тогда существует область сходимости ряда (2.103):
; тогда существует область сходимости ряда (2.103): ![]() , которую обозначим через G. Тогда как ряд (2.104) сходится равномерно на всяком замкнутом множестве в круге
, которую обозначим через G. Тогда как ряд (2.104) сходится равномерно на всяком замкнутом множестве в круге ![]() , и преобразование
, и преобразование  переводит всякое замкнутое множество точек указанного круга в некоторое замкнутое множество точек области G. В этой области ряд (2.103) определяет функцию:
переводит всякое замкнутое множество точек указанного круга в некоторое замкнутое множество точек области G. В этой области ряд (2.103) определяет функцию:
![]() (2.105)
(2.105)
аналитическую во всех точках области G. В бесконечно удаленной точке g(z) принимает значение ![]() . Будем по определению называть функцию g(z) аналитической в бесконечно удаленной точке.
. Будем по определению называть функцию g(z) аналитической в бесконечно удаленной точке.
Следовательно, аналитичность функции в z=¥ характеризуется наличием в разложении ряда вида (2.105).
Определение. Ряд вида
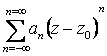 , (2.106)
, (2.106)
где z0 – фиксированная точка комплексной плоскости, an – заданные комплексные числа, называется рядом Лорана . Этот ряд сходится в точке z, если в этой точке сходятся ряды:
![]() (правильная часть ряда Лорана) (2.107)
(правильная часть ряда Лорана) (2.107)
и
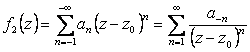 (главная часть ряда Лорана), (2.108)
(главная часть ряда Лорана), (2.108)
а сумма ![]() ряда (V.3.4) по определению равна сумме рядов (2.107) и (2.108), т.е.
ряда (V.3.4) по определению равна сумме рядов (2.107) и (2.108), т.е. ![]() .
.
Теорема. Функцию, аналитическую в кольце ![]() , можно разложить в ряд по положительным и отрицательным степеням разности z – z0, сходящийся во всех точках кольца (2.106) или в развернутом виде:
, можно разложить в ряд по положительным и отрицательным степеням разности z – z0, сходящийся во всех точках кольца (2.106) или в развернутом виде:
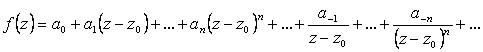 (2.109)
(2.109)
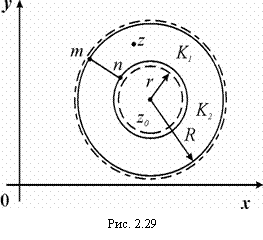 Для доказательства возьмем произвольную точку z внутри кольца
Для доказательства возьмем произвольную точку z внутри кольца ![]() и проведем две концентрические окружности К1 и К2 так, чтобы z лежала между ними (рис. 2.29). Сделаем разрез mn. Получим контур L: К1 + mn + К2 + nm, который ограничивает односвязную область D. Функция
и проведем две концентрические окружности К1 и К2 так, чтобы z лежала между ними (рис. 2.29). Сделаем разрез mn. Получим контур L: К1 + mn + К2 + nm, который ограничивает односвязную область D. Функция ![]() аналитическая в области
аналитическая в области ![]() (область D¢ обозначена штриховой линией). По интегральной формуле Коши:
(область D¢ обозначена штриховой линией). По интегральной формуле Коши:
![]()
По свойству аддитивности:
 (2.110)
(2.110)
Так как контур mn проходится в двух противоположных направлениях и подынтегральные выражения в интегралах совпадают, то интегралы, берущиеся по этим контурам, взаимно уничтожаются. Обход в третьем интеграле заменим на противоположный, из (2.110) получим:
 (2.111)
(2.111)
В первом интеграле переменная zÎК1, а z находится внутри контура, поэтому ![]() , а дробь
, а дробь ![]() разлагаем в ряд, представляющий сумму членов бесконечно убывающей геометрической прогрессии со знаменателем
разлагаем в ряд, представляющий сумму членов бесконечно убывающей геометрической прогрессии со знаменателем 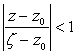 :
:

Следовательно,
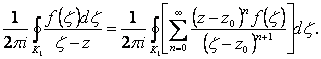 (2.112)
(2.112)
Законность интегрирования ряда гарантируется построением мажорантного числового сходящегося ряда и признаком Вейерштрасса и сравнения. Поэтому
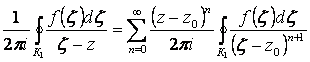 . (2.113)
. (2.113)
Обозначим
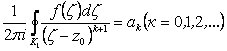 . (2.114)
. (2.114)
Окончательно:
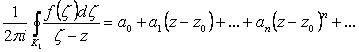 (2.115)
(2.115)
Аналогично, во втором интеграле переменная zÎК2, а точка z лежит вне К2, поэтому ![]() , а дробь
, а дробь 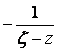 разлагается в ряд:
разлагается в ряд:

Интегрируя почленно ряд, получим:
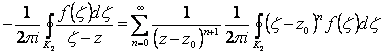 . (2.116)
. (2.116)
Обозначив
 (2.117)
(2.117)
получим:
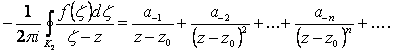 (2.118)
(2.118)
Равенства (2.111), (2.115), (2.118) дают разложение (2.109).
Формулы для коэффициентов ряда Лорана объединяем в одну:
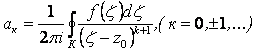 , (2.119)
, (2.119)
где К – произвольная кривая кольца ![]() .
.
Методические замечания
а) Имеет место свойство единственности разложения в ряд Лорана. Это значит, что каким бы способом ни разлагали, ряд Лорана будет одним и тем же.
б) Для нахождения коэффициентов ряда Лорана редко пользуются формулой (2.119). Функцию ![]() , аналитическую в кольце
, аналитическую в кольце ![]() , представляют в виде суммы или произведения двух функций (если это возможно):
, представляют в виде суммы или произведения двух функций (если это возможно):![]() или
или ![]() , из которых одна, например,
, из которых одна, например, ![]() аналитическая внутри большого круга
аналитическая внутри большого круга ![]() , другая –
, другая – ![]() – вне меньшего круга
– вне меньшего круга ![]() . Первую разлагают по
. Первую разлагают по
положительным, а вторую по отрицательным степеням разности ![]() . Результаты остается сложить или перемножить.
. Результаты остается сложить или перемножить.
Пример 1
Разложить 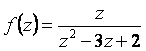 по степеням z в ряд Лорана в кольце
по степеням z в ряд Лорана в кольце ![]() .
.
Решение. Функция ![]() – аналитическая в кольце
– аналитическая в кольце ![]() . Имеет две особые точки: z = 1 и z = 2. Разобьем функцию на сумму двух, из которых одна – аналитическая в круге
. Имеет две особые точки: z = 1 и z = 2. Разобьем функцию на сумму двух, из которых одна – аналитическая в круге ![]() . Для этого разложим данную дробь на сумму простейших, найдем:
. Для этого разложим данную дробь на сумму простейших, найдем:
![]() .
.
Дробь ![]() разложим в круге
разложим в круге ![]() по положительным степеням z:
по положительным степеням z:
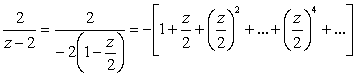 .
.
Дробь ![]() разложим в круге
разложим в круге ![]() :
:
 .
.
Следовательно,
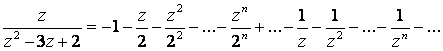
![]()
Пример 2
Разложить ![]() по положительным и отрицательным степеням z в кольце
по положительным и отрицательным степеням z в кольце ![]() .
.
Решение. Для конечного z ¹ 0 имеем:
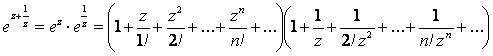 .
.
Перемножим выражения в правой части уравнения, найдем, что коэффициенты ![]() при
при ![]() и
и ![]() при
при ![]() одинаковы:
одинаковы:
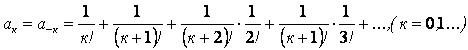 .
.
Пример 3
Разложить ряд Лорана функцию ![]() по степеням z в окрестности:
по степеням z в окрестности:
а) z=0; б) ![]() .
.
Решение
а) Выполним тождественные преобразование, которое приводит к использованию суммы членов бесконечно убывающей прогрессии:
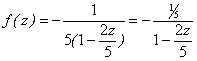 .
.
Поскольку ![]() , то
, то
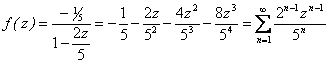 .
.
Разложение содержит только правильную часть. Из ![]() следует, что область сходимости ряда есть круг
следует, что область сходимости ряда есть круг ![]() .
.
б) Выполним тождественное преобразование с той же целью как в предыдущем примере:
 .
.
Видно, что в окрестности ![]() выполняется неравенство
выполняется неравенство ![]() . Следовательно, функция f(z) представима в виде ряда
. Следовательно, функция f(z) представима в виде ряда
![]() .
.
Разложение не содержит правильной части. Ряд сходится в области ![]() .
.
Пример 4
Разложить в ряд Лорана функцию ![]() по степеням z – 2.
по степеням z – 2.
Решение. Сделаем замену z – 2 = t. Тогда
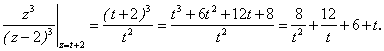
Возвращаясь к старой переменной z, получим:
![]()
Главная часть содержит два члена; правильная часть – три. Имеем многочлен. Следовательно, разложение верно для всех z, кроме z = 2.
Пример 5
Функцию ![]() разложить в ряд Лорана в окрестности точки z = 0.
разложить в ряд Лорана в окрестности точки z = 0.
Решение. Используем известное разложение
![]() .
.
Тогда ряд Лорана для данной функции в окрестности точки z = 0 будет:
![]()
Главная часть есть
![]() ,
,
а правильная часть равна
![]() .
.
Пример 6
Разложить в ряд Лорана функцию ![]() в окрестности особой точки.
в окрестности особой точки.
Решение. Особая точка функции есть z=0. В окрестности этой точки ![]() представляется рядом:
представляется рядом:
![]()
тогда
![]()
значит
![]()
Главная часть ряда содержит бесконечное число слагаемых, а правильная два.
Пример 7
Разложить функцию ![]() в ряд Лорана.
в ряд Лорана.
Решение. Из курса элементарной алгебры известно правило деления расположенных многочленов. Если многочлены нацело не делятся, то алгоритм можно применять бесконечно, и в результате получится ряд. Деля многочлены «столбиком» получим:
![]() .
.
Это есть ряд Лорана, который сходится в кольце 0<|z|<1, так как особые точки ![]() : z=0, z=i, z=-i, и функция аналитическая в указанном кольце.
: z=0, z=i, z=-i, и функция аналитическая в указанном кольце.
Пример 8
Разложить ![]() в ряд Лорана.
в ряд Лорана.
Решение. Аналогично предыдущему примеру, после деления многочленов, получим:
![]()
Ряд сходится в кольце ![]() , так как особые точки функции находятся в точках
, так как особые точки функции находятся в точках ![]() , модуль каждого из этих чисел равен единице.
, модуль каждого из этих чисел равен единице.