Рассмотрим, как применяется непосредственно (3.1) и свойства 1 – 6 преобразования Лапласа.

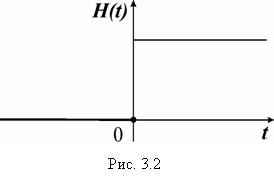
1) Единичная функция Хевисайда (рис. 3.2):

                        (3.9)

При :

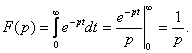
Итак,

1.                               (3.10)

2) Изображение независимой переменной f(t) = t. При , интегрируя по частям, имеем:

.

Итак,

t .                                                               (3.11)

Соотношение (3.11) обобщается на случай, когда , n – целое положительное число:

Итак,

                                                            (3.12)

3) Изображение показательных функций. Пусть , тогда

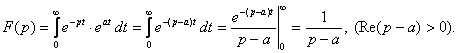          (3.13)

Аналогично,

                                                          (3.14)

В (3.13) и (3.14) можно сослаться на свойство смещения.

4) Изображения гиперболических функций. Известно, что

; .

Применяя свойство линейности к  получим:

                   (3.15)

Аналогично для :

                                      (3.16)

Итак,

 ;   .

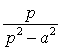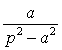5) Изображение тригонометрических функций. Известно, что

Используя (3.15), получим:

                                (3.17)

                             (3.18)

6) Изображение функций  и .

Используя свойство смещения, получим:

.                                          (3.19)

                                           (3.20)

Соответствия (3.19) и (3.20) есть изображения затухающих колебаний (рис. 3.3).

7) Изображение функции .

Применяя последовательно свойства линейности и смещения, найдем:

Итак,

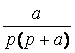                                                  (3.21)