Основная идея метода Гаусса заключается в следующем: по исходной системе линейных уравнений  строим другую систему линейных уравнений , имеющую то же решение x, что и первая, но матрица которой  является верхней треугольной матрицей. А затем решаем систему линейных уравнений с верхней треугольной матрицей.

Метод Гаусса состоит из двух этапов:

1 Прямой ход метода  Гаусса. Прямой ход метода  Гаусса заключается в преобразовании исходной системы линейных уравнений к эквивалентной системе линейных уравнений с верхней треугольной матрицей.

2. Обратная подстановка. Обратная подстановка метода  Гаусса заключается в решении системы линейных уравнений с верхней треугольной матрицей. При этом компоненты вектора решения находятся в обратном порядке .

С точки зрения операций над матрицами метод Гаусса заключается в разложении исходной матрицы А в произведение двух треугольных матриц: нижней треугольной матрицы , на диагонали которой стоят единицы, и верхней треугольной матрицы  с ненулевыми диагональными элементами:

,

,              ,   ,                     ,   .

.

Другими словами, вместо системы линейных уравнений  решается две системы линейных уравнений с треугольными матрицами:

Ly = b,

Ux = y.

Определение. Элементы, расположенные на главной диагонали верхней треугольной матрицы , полученной после выполнения прямого хода метода Гаусса, называют ведущими элементами.

Теорема

Для существования -разложения матрицы А необходимо и достаточно, чтобы у матрицы А все главные миноры были отличны от нуля.

Мы будем рассматривать: метод Гаусса без выбора ведущего элемента, метод Гаусса с частичным выбором ведущего элемента и метод Гаусса с полным выбором ведущего элемента. В методе Гаусса без выбора ведущего элемента исходная матрица A представляется в виде произведения двух треугольных матриц LU.

Следствие. Метод Гаусса без выбора ведущего элемента можно применять в том случае, когда все главные миноры матрицы системы линейных уравнений отличны от нуля.

Пример 1

Рассмотрим матрицу .

Определитель матрицы не равен нулю (det(A)0), но первый главный минор равен нулю, следовательно, -разложение матрицы А невозможно. Система линейных уравнений с этой матрицей имеет единственное решение, но оно не может быть получено методом Гаусса без выбора ведущего элемента.

Пример 2

Решить систему линейных уравнений методом Гаусса без выбора ведущего элемента:

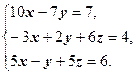
Решение

Прямой ход

М₁ = 10,     М₂ = -1,     М₃ = -155, где М_i – главные миноры матрицы A. Все главные миноры отличны от нуля, следовательно, можно применять метод Гаусса без выбора ведущего элемента.

Нам необходимо, используя эквивалентные преобразования, получить верхнюю треугольную матрицу.

Вместо  необходимо получить ноль. Для этого умножим первое уравнение на такое число, чтобы при сложении этого уравнения со вторым исключилось неизвестное .

Умножим  первое уравнение на 0.3 и прибавим ко второму. Умножим первое уравнение на  –0.5 и прибавим к третьему. Получим:

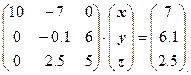
Умножили второе уравнение на 25 и прибавим к третьему. Получим:

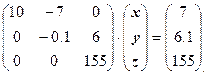
Мы получили систему линейных уравнений с верхней треугольной матрицей.

Обратная подстановка

,                  следовательно, z =1.

,           следовательно, .

,        следовательно, .

Пример 3

Записать -разложение матрицы А.

Решение

Рассмотрим матрицу А из предыдущего примера. U – верхняя треугольная матрица, полученная в результате прямого хода. L – нижняя треугольная матрица, на главной диагонали которой расположены единицы. Ненулевые элементы матрицы  – это множители, используемые на шагах исключения, с противоположным знаком:

;         ;                       ;           ;

;             .

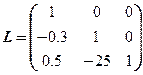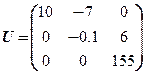Проверка:

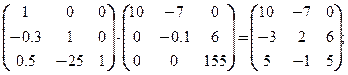
Ведущие элементы 10,  -0.1,  155.

Формулы метода Гаусса

Прямой ход

;                        .

      .

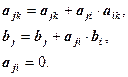
Обратная подстановка

                    .

              .

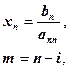
Нахождение значения определителя матрицы методом Гаусса без выбора ведущего элемента

, следовательно, .

Если Т – треугольная матрица размерности n, то , где t_ii – диагональные элементы матрицы T.

Определитель треугольной матрицы равен произведению ее элементов, расположенных на главной диагонали.

,          .

Определитель матрицы А, у которой все главные миноры отличны от нуля, равен произведению ее ведущих элементов, вычисленных методом Гаусса без выбора ведущего элемента.

Пример 4

Найти значение определителя матрицы.

Решение

Рассмотрим матрицу из примера 2:

Отметим, что если один из главных миноров матрицы А равен нулю, то при попытке решить систему линейных уравнений мы получим деление на ноль (). Это первый недостаток метода Гаусса без выбора ведущего элемента.

Второй недостаток: если какой-либо из ведущих элементов принимает малые значения по модулю, то вычислительный алгоритм метода Гаусса без выбора ведущего элемента становится неустойчивым.

Правило. Если ведущие элементы в методе Гаусса по модулю больше, либо равны 1, то ошибки округления в процессе вычисления подавляются, в противном случае ошибки округления увеличиваются.

Условие устойчивости: .

Сложность метода Гаусса без выбора ведущего элемента

Число арифметических действий, необходимых для реализации метода Гаусса без выбора ведущего элемента пропорционально n³, где n – число линейных уравнений. Записывается это так: , где NA – число арифметических действий. Объем памяти, необходимый для реализации алгоритма, пропорционален  – .

Введем понятие невязки или вектора невязки

Определение. Невязкой или вектором невязки называется вектор: , где  – вычисленное решение системы линейных уравнений .