Пусть задана система нелинейных уравнений:

             или в векторном виде:     F(x) = 0.

Требуется найти приближенное значение решения системы нелинейных уравнений такое, что

, где     – приближенное решение;            c – точное решение.

Рекомендуемая литература: /3-8, 10, 15/.

Задача может ставиться по-разному: найти все решения, найти хотя бы одно решение. Отметим, что решение системы нелинейных уравнений является существенно более сложной задачей, чем решение системы линейных уравнений. Для системы нелинейных уравнений возможны четыре случая:

1) система нелинейных уравнений имеет единственное решение;

2) система нелинейных уравнений не имеет решения;

3) система нелинейных уравнений имеет бесконечное множество решений;

4) система нелинейных уравнений имеет несколько решений.

Вопрос о существовании и количестве решений системы нелинейных уравнений в общем случае является сложным. Приведём пример из /3/.

Пример

Рассмотрим систему нелинейных уравнений:

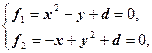
где d – вещественный параметр, -1 £ d £ 1. Если изменять d в указанном интервале, то имеют место следующие случаи:

1)    d = -1         – четыре решения;

2)    d = 0           – два решения;

3)    d = 0.25      – решение единственно;

4)    d = 1            – решений нет.

Как и при решении одного нелинейного уравнения задача разбивается на две подзадачи:

1) отделение решения, то есть нахождение некоторых областей D_i, каждая из которых содержит одно и только одно решение системы нелинейных уравнений, , где m – число решений системы нелинейных уравнений;

2) в известной области D, содержащей одно решение системы нелинейных уравнений, ищется приближенное решение с заданной точностью e. Этот этап называется уточнением решения.

Отметим, что мы будем рассматривать два итерационных метода – метод итераций и метод Ньютона. Оба эти метода можно использовать тогда, когда известна выпуклая область D, содержащая одно решение системы нелинейных уравнений.

Определение. Область называется выпуклой, если отрезок прямой, соединяющий две любые точки области, полностью принадлежит области.

Примеры выпуклых областей:  круг, квадрат, прямоугольник, эллипс, куб, параллелепипед, конус, сфера.

Таким образом, на первом этапе нам необходимо отделить выпуклую область D, содержащую одно решение системы нелинейных уравнений.