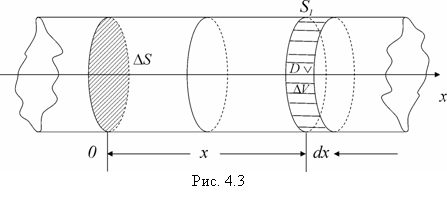
Рассмотрим однородный стержень (под стержнем в механике понимается тело с одним превалирующим линейным размером, например, столб можно рассматривать как стержень с переменным сечением) постоянного поперечного сечения S и длины l, теплоизолированный с боков, ось которого примем за ось Ох (рис. 4.3). Обозначим через U(x,t)  температуру стержня в сечении с абсциссой х в момент времени t (предполагается, что во всех точках любого поперечного сечения стержня температура одна и та же.

Пусть  – плотность стержня,  – его удельная теплоемкость (это количество калорий, которое необходимо, чтобы единицу массы стержня нагреть на 1 ºС),  – коэффициент теплопроводности (он представляет собой количество тепла в калориях, которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на 1 ºС при перемещении вдоль стержня на единицу длины),  – интенсивность теплового источника, находящегося в сечении х для момента t, отнесенная к единице массы и единице времени (т.е. количество тепла, создаваемого этим источником тепла за единицу времени и приходящегося на единицу массы; например, лампочку включенную в помещении, аппаратуру, работающую на космическом корабле и др. можно рассматривать как источники тепла;). Температуру же U(x, 0) стержня в начальный момент времени мы считаем известной и обозначим её через :

.                                                      (4.35)

Тепловой режим на концах стержня может быть весьма разнообразен, т.е. температура может быть и постоянной, и изменяться, например, по законам:   и др.). Мы рассмотрим два случая:

1) концы стержня поддерживаются при постоянной нулевой температуре:

;                                                 (4.36)

2) концы стержня находятся в той же теплоизолирующей оболочке, что и весь стержень. Это означает, что через концы не происходит протекание тепла.

Рассмотрим сечение х нашего стержня и найдем, какое количество Q тепла протечет (слева направо) через это сечение за элементарный промежуток времени . В момент t температура стержня в точке х будет равна . Возьмем отличную от точки х точку  x + dx  стержня (пусть для определенности dx > 0) согласно закону Фурье количество тепла, протекающего в направлении оси Ох за бесконечно малый промежуток времени dt через сечение S с абсциссой х, будет:

,                                                      (4.37)

где k – коэффициент теплопроводности ( представляет здесь величину градиента температуры U). Во формуле (4.37) стоит знак минус, так как при , т.е. при росте U вместе с х, поток тепла направлен в противоположную сторону, и наоборот).

Составим тепловой баланс для элемента , заключенную между бесконечно близкими сечениями  х  и  x + dx.  Предположим для определенности, что U возрастает в направлении Ох. Тогда через сечение с абсциссой х тепло выходит, а через сечение с абсциссой  x + dx  входит. Пусть dQ есть количество тепла, накопленное нашим элементом  за время dt. Тогда количество тепла, созданное за dt источниками тепла в элементе  равно:

.                                                    (4.38)

Используя формулу (4.37) будем иметь:

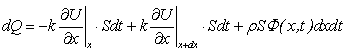.                            (4.39)

Применяя формулу Лагранжа из дифференциального исчисления  с точностью до бесконечно малых высшего порядка малости, получим:

.

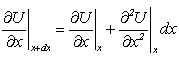Следовательно, формула (4.39) примет вид:

.                                        (4.40)

С другой стороны,  есть скорость изменения температуры элемента , и поэтому  представляет собой изменение его температуры. Так как масса элемента  равна , то накопленное при этом количество тепла будет:

.                                                     (4.41)

Итак, сравнивая (4.41) и (4.40), после сокращения получим:

                                              (4.42)

или, обозначая  (величина а называется коэффициентом температуропроводности), окончательно получим дифференциальное уравнение, описывающее распределение температуры U(x,t) в стержне и носит название уравнения теплопроводности:

                                             (4.43)

Если источники тепла отсутствуют, то уравнение (4.43) принимает вид уравнения свободного теплообмена в стержне:

.                                                          (4.44)

Аналогичным образом можно вывести уравнения для распространения температуры в пластине:

;

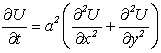и в тепле

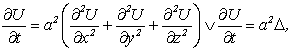
где        – оператор Лапласа (см. разд. 1.4.6).

Вывод: уравнение теплопроводности есть уравнение с частными производными второго порядка, параболического типа, так как ; в процессе вывода уравнения теплопроводности мы пришли к двум математическим задачам:

1) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям (4.36).

2) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям:

                                                     (4.45)

т.е. когда концы стержня теплоизолированы (количество тепла, протекающее через них, равно нулю).