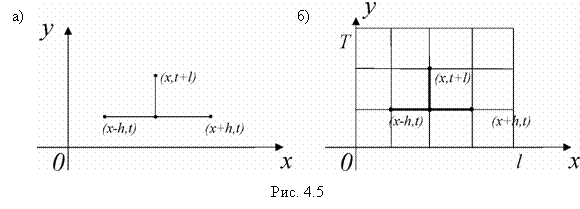
На практике часто приходится решать уравнения с частными производными методом конечных разностей (МКР). При этом производные заменяются соответствующими разностями (рис. 4.5.)
; (4.61)
или
(4.62)
(4.63)
Первая краевая задача для уравнения (4.44) формулируется так: требуется найти решение уравнения (4.44), удовлетворяющее краевым условиям:
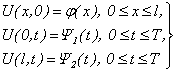(4.64)
т.е. требуется найти решение U(x, t) в прямоугольнике, ограниченном прямыми t = 0, x = 0, x = l, t = T, если заданы значения искомой функции на трех его сторонах: t = 0, x =0, x = l (рис. 4.5).
Покроем нашу область прямоугольной сеткой, образованной прямыми x = ih, t = kl (i, k = 1, 2,…), и будем определять приближенные значения решения в узлах сетки. Введем обозначения: 
. Напишем вместо уравнения (4.44) соответствующее ему уравнение в конечных разностях для точки 
, получим (для (4.64)):
. (4.65)
Найдем
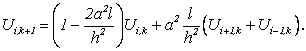(4.66)
Из формулы (4.66) следует, что если известны три значения в k-м ряду 
, то определяется значение 
в k+1-м ряду (слое). Нам известны все значения на прямой t = 0. Значения в крайних точках этого отрезка нам известны в силу (4.64). Так, ряд за рядом мы определим значения искомого решения во всех узлах сетки [18].
Формула (4.66) упрощается, если шаг l по оси t выбрать так, чтобы 
или 
. В этом случае уравнение (4.66) будет:
(4.67)
Указанным методом решение определяется в узлах сетки. Решение между узлами сетки можно получить, например, экстраполированием, проводя плоскость через каждые три точки в пространстве (x, t, u).
Замечание. По аналогии с одномерным случаем вывода уравнения теплопроводности легко можно получить уравнение теплообмена в пространстве и на плоскости.
Методическое руководство
Элемент стержня 
следует заменить на элемент объема 
. Количество тепла, затраченное на повышение температуры за dt заменяется на 
, а общее количество тепла, затраченное на повышение температуры в объёме за время dt, будет 
, но, с другой стороны, это тепло, поступившее в объем 
за время dt, определяется: 
, где 
– единичный вектор нормали к поверхности S, ограничивающей объем 
. Баланс дает:
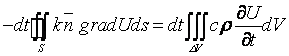
(здесь использовали формулу Остроградского из векторного анализа). Заменяя поверхностный интеграл тройным, получим:
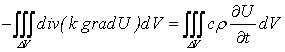
или
.
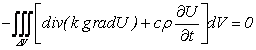Применив теорему о среднем, получим:
для некоторой точки объема 
. Но мы выделили произвольный объем в пространстве, где идет процесс передачи тепла, а подынтегральная функция непрерывна, поэтому последнее равенство имеет место в каждой точке пространства:
.
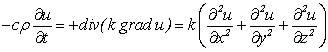Положив 
,
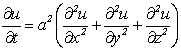(4.68)
или
(4.69)
где 
– оператор Лапласа. Уравнение (4.68) и есть уравнение теплопроводности в пространстве. Для нахождения его единственного решения задают краевые условия.
Если искомая функция U(x,y,z,t) не зависит от z, то получаем уравнение теплопроводности тепла на плоскости:
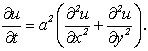(4.70)