Погашение долгосрочной ссуды возможно не только единовременным платежом, но и множеством распределенных во времени выплат. В финансовой литературе ряд распределенных во времени выплат и поступлений называется потоком платежей.

Потоки платежей являются неотъемлемой частью всевозможных финансовых операций:

· с ценными бумагами;

· в управлении финансами предприятий;

· при осуществлении инвестиционных проектов;

· в кредитных операциях;

· при оценке бизнеса;

· при оценке недвижимости;

· при выборе альтернативных вариантов финансовых операций и т. п.

Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а периоды между членами могут быть равными и неравными.

Финансовая рента (аннуитет) – поток платежей, все члены которого имеют одинаковое направление (т.е. знак), а периоды между последовательными платежами постоянны.

При рассмотрении финансовой ренты используются основные категории:

· член ренты (R)– величина каждого отдельного платежа;

· период ренты (t)– период между членами ренты;

· срок ренты (n)– время от начала финансовой ренты до конца последнего ее периода;

· процентная ставка (i)– ставка, используемая при наращении платежей, из которых состоит рента.

Так как условия финансовых сделок весьма разнообразны, поэтому разнообразны и виды финансовых рент. Классификация финансовых рент представлена на рисунке 5.1.

Для всех перечисленных финансовых потоков (см. рисунок 5.1) обобщающими характеристиками являются:

1) наращенная сумма;

2) современная величина потока платежей.

Рассмотрим каждую из этих характеристик.

Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т.п.

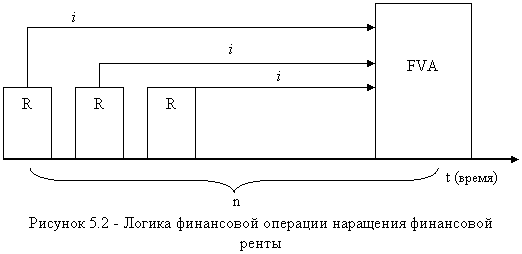
Логику наращения финансовой ренты можно представить схемой (рисунок 5.2). Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом, равным R, и множителем, равным (1 + i).

Рассмотрим определение наращенной суммы на примере наиболее простого случая – годовой постоянной обычной ренты. Наращенная сумма годовой постоянной обычной ренты определяется по формуле:

, (5.1)

где FVA– наращенная сумма ренты; R– размер члена ренты, т.е. размер очередного платежа; i– годовая процентная ставка, по которой на платежи начисляются сложные проценты; n– срок ренты в годах; s_n;i– коэффициент наращения ренты.

Пример 1

На счет в банке в течение пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30 %. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение

Поскольку период ренты равен одному году, то это годовая рента. Проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента. Сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты. Число членов ренты пять, т.е. конечно, следовательно, рента ограниченная; а выплаты носят безусловный характер. Таким образом, это верная рента.

Сумма всех взносов с начисленными процентами определяется по формуле (5.1):

;

руб.

Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами, содержащими коэффициенты наращения ренты:

FVA = R · s_{5; 30};

FVA = 500 · 9,0431 = 4 521,55 руб.

Сумма взносов в течение 5 лет составит:

P = n · R;

FVA = 5 · 500 = 2 500 руб.

Следовательно, сумма начисленных процентов будет равна:

I = FVA – P;

I = 4 521,55 – 2 500 = 2 021,55 руб.

Таким образом, доход владельца счета за 5 лет составит 2 021,55 руб.

Для овладения методами финансовой математики важно не столько запоминание формул, сколько понимание общих принципов расчета.

Для определения наращенной суммы на конец рассматриваемого периода последовательно присоединяются промежуточные результаты наращения к очередному платежу.

Рассмотрим поэтапное решение примера 1 (таблица 5.1).

Таблица 5.1 Расчет наращенной величины аннуитета

Период	Взносы*	Проценты, начисленные за период	Наращенная сумма на конец периода
1	500,00	-	500,00
2	500,00	150,00	1150,00
3	500,00	345,00	1995,00
4	500,00	598,50	3093,50
5	500,00	928,05	4521,55
* Взносы поступают в конце периода.

Таким образом, получается такая же сумма, как и по формуле наращения аннуитета (5.1). Однако рассматриваемая формула используется только при начислении процентов один раз в год, но возможны случаи и неоднократного начисления процентов в течение года, тогда используют следующую формулу:

,                                             (5.2)

где j– номинальная ставка процентов.