Рассмотрим функцию  на отрезке  и последовательность интерполяционных полиномов   Возникает вопрос: существует ли для точки  предел этой последовательности и равен ли он значению: ?

Определение. Интерполяционный полином  сходится к функции  для  , если  .

Рассмотрим два примера.

Рис. 5.2. Интерполяция функции Рунге

Пример 1 (Рунге)

В 1901 г. Рунге (1901 г.) рассмотрел интерполяцию полиномами на отрезке  функции    при равномерном распределении узлов сетки. Выяснилось, что при бесконечном увеличении степени n интерполяционного полинома , последовательность  расходится на интервале  (рис. 5.2). То есть

.

При этом  – достаточно «хорошая», гладкая функция.

Чем выше степень интерполяционного полинома, построенного по интерполяционной таблице с равномерным шагом для функции , тем больше погрешность.

Пример 2 (Бернштейн, 1912 г.)

Последовательность интерполяционных полиномов , построенных на равномерных сетках ,  для непрерывной функции , не стремится с возрастанием n к функции  ни в одной точке отрезка , отличной от  -1, 0,1 (рис. 5.3).

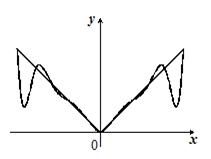
Рис. 5.3. Интерполяция функции y = |x|

Эти два примера иллюстрируют недостаток интерполяции полиномами:  с увеличением степени интерполяционного полинома возможны существенные отклонения интерполяционного полинома от функции на концах интервала. Увеличение степени полинома накладывает все более жесткие ограничения на  .

Теорема Фабера

Для любой интерполяционной таблицы размерности  найдутся непрерывная функция  и точка , такие, что  не сходится к функции  в точке  при .