Введем несколько определений.
Определение. Квадратурной формулой называется всякая простая формула, аппроксимирующая отдельный интеграл 
:
, 
.
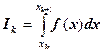Таким образом, любая формула для нахождения 
– это квадратурная формула.
Определение. Составная квадратурная формула – это формула, дающая приближение к интегралу
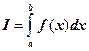
в виде суммы приближений по данной квадратурной формуле к отдельным интегралам :
, 
.
Часто вместо «составная квадратурная» формула говорят просто: «формула».
Рассмотрим две простейшие квадратурные формулы: трапеций и прямоугольников.
Квадратурная формула трапеций
Квадратурная формула трапеций аппроксимирует интеграл: .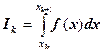
Заменяем площадь «маленькой» криволинейной трапеции площадью обычной трапеции (рис. 6.2).
Квадратурная формула трапеций:
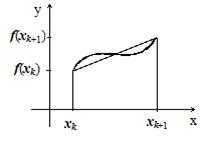
Рис. 6.2. Квадратурная формула трапеций
, 
.
, где 
– погрешность квадратурной формулы.
Пояснение. Если 
для 
, то 
, где с – константа.
Составная квадратурная формула трапеций
Будем считать, что сетка задана с постоянным шагом 
.
Запишем интеграл в виде:
, где 
, 
.
Здесь
– составная квадратурная формула трапеций:
, 
;
– остаточный член или погрешность формулы трапеций:
, где с – некоторая точка из 
;
.
Квадратурные формулы прямоугольников
Квадратурная формула прямоугольников – 
.
Формула левых прямоугольников: 
, 
(рис. 6.3,а).
Формула правых прямоугольников: 
(рис. 6.3,б).
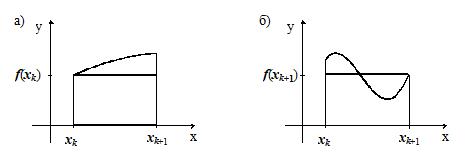
Рис. 6.3. Квадратурная формула левых (а) и правых (б) прямоугольников
Формула средних прямоугольников (рис. 6.4):
, .
,
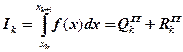где 
– погрешность квадратурной формулы прямоугольников; 
.
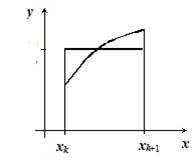
Рис. 6.4. Квадратурная формула средних прямоугольников
Составная квадратурная формула прямоугольников
Запишем интеграл I в виде суммы
, где 
– составная квадратурная формула прямоугольников, 
– остаточный член или погрешность формулы прямоугольников
, 
.
Считая шаг сетки постоянным 
, получаем составную квадратурную формулу прямоугольников:
.
Запишем формулу для погрешности 
, где с – некоторая точка из 
.
.
Недостатком формулы прямоугольников является необходимость вычисления значения 
в средних точках.