Отметим, что погрешность всех рассмотренных нами составных квадратурных формул удовлетворяют неравенству , где , не зависящая от h, а p – целое положительное число.

Определение. Число p называют порядком остаточного члена (погрешности) составной квадратурной формулы.

Для формулы трапеций и формулы прямоугольников p = 2. Для формулы Симпсона p = 4.

Если нам задана формула функции , то мы можем оценить погрешность, используя формулы остаточных членов. Если же формула функции  не задана, то можно использовать правило Рунге.

В вычислительной математике есть общее правило: если нам известны два приближенных значения одного и того же точного значения, то модуль разности этих двух приближенных значений, деленный на некоторую константу, является оценкой погрешности вычисления точного значения.

Правило Рунге. Разность результатов, полученных по одной и той же составной квадратурной формуле, до и после удвоения числа элементарных отрезков, можно использовать, чтобы оценить погрешность численного интегрирования.

,

где         – значение составной квадратурной формулы для интервалов,

   – значение составной квадратурной формулы для интервала,

p        – порядок остаточного члена составной квадратурной формулы,

 – оценка погрешности численного интегрирования для  интервала; .

Для формулы прямоугольников и трапеций

.

Для формулы Симпсона

.

Отметим, что правило Рунге используется и тогда, когда формула  задана.

Экстраполяция по Ричардсону. Пусть  и  – два приближенных значения интеграла 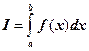 , найденных по одной и той же составной квадратурной формуле при числе отрезков n и m (m > n). Тогда более точное приближенное значение этого интеграла можно найти по формуле:

,

где     p – порядок остаточного члена выбранной составной квадратурной формулы;

p = 2  для формулы трапеций и формулы прямоугольников;

p = 4 для формулы Симпсона.

Если m = 2n , то  .