Рассмотрим несколько формул, аппроксимирующих первую производную y¢. Эти формулы можно использовать для численного дифференцирования и для построения разностных задач.

Рассмотрим равномерную сетку:

,     ,     ,     .

Предположим, что функция  является дважды непрерывно дифференцируемой на . Тогда для первой производной справедлива формула дифференцирования вперёд:

,       .

Обычно под формулой численного дифференцирования понимают приближенное равенство:

.

Разность

называется погрешностью аппроксимации. Если , то R = O(h), то есть , где c – константа, большая нуля, не зависящая от h. Другими словами, формула дифференцирования вперёд аппроксимирует первую производную с первым порядком по h.

Используя формулу дифференцирования вперёд, запишем разностную задачу (разностную схему) для дифференциальной задачи Коши:

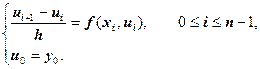
Эта разностная задача называется явной схемой Эйлера.

Аналогично дифференцированию вперёд для дважды непрерывно дифференцируемой на  функции y справедлива формула дифференцирования назад:

,         .

Получаем приближённое равенство:

,

которое является формулой численного дифференцирования. Для  погрешность аппроксимации R = O(h), то есть , где c – константа, большая нуля,

не зависящая от h. Другими словами, формула дифференцирования назад аппроксимирует первую производную с первым порядком по h.

Используя формулу дифференцирования назад, запишем разностную задачу (разностную схему) для дифференциальной задачи Коши:

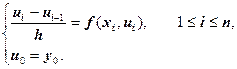
Эта разностная задача называется явной схемой Эйлера.

Термин «явная» и «неявная» схемы связаны с тем, что явная схема, например явная схема Эйлера, даёт возможность найти  по явной формуле:

,

где  – известная величина. В случае неявной схемы получается уравнение, в котором неизвестное  входит и в левую, и в правую часть:

.

Явные схемы удобны тем, что по ним легко находятся неизвестные значения .

Формулу дифференцирования вперёд называют ещё правой разностью, формулу дифференцирования назад – левой разностью. А для  справедлива формула численного дифференцирования, называемая центральной разностью:

,     .

Центральная разность аппроксимирует первую производную со вторым порядком по h.

Запишем формулы, аппроксимирующие первую производную со вторым порядком по h на концах отрезка (в точках  и ):

,

.