Рассмотрим погашение единовременным платежом. В простейшем случае кредит погашается единым платежом в конце срока:
Y = D (1 + i)n,
где Y– срочная уплата; D– сумма долга.
Этот платеж, как наращенная сумма долга, состоит из двух частей:
· возврата основной суммы долга (D);
· выплаты процентов по долгу (I)
I = D (1 + i)n – D.
В финансовой практике встречаются случаи, когда у кредитора возникает необходимость вернуть часть денег досрочно. В таких случаях возникает риск невозврата, поскольку требуемой суммы на такой момент времени может и не быть.
При значительной сумме долга разовый платеж требует создания так называемого фонда погашения путем периодических взносов. Фонд погашения аккумулирует денежные средства, направленные на погашение задолженности. Наиболее эффективно размещение фонда погашения с начислением на взносы процентов, например, на специальном счете в банке. Нетрудно заметить, что такие платежи по своей сути являются финансовой рентой (аннуитетом), поэтому задача сводится к определению одного из параметров финансовой ренты – члена ренты. Здесь возможно два варианта:
1) выплата процентов по мере их начисления, возвращение основной суммы денег в конце срока займа;
2) погашение долга единовременным платежом с помощью создания фонда.
При первом варианте выплата процентов производится по мере их начисления, а основная сумма денег возвращается в конце срока займа (рисунок 6.1).
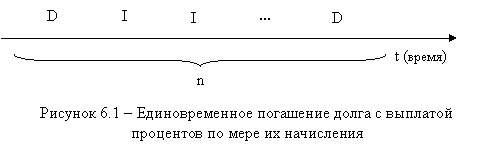 Если проценты выплачиваются ежегодно, тогда величина срочной уплаты (расходов должника по погашению долга) равна:
Если проценты выплачиваются ежегодно, тогда величина срочной уплаты (расходов должника по погашению долга) равна:
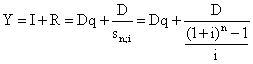 , (6.1)
, (6.1)
где D– первоначальная сумма долга; q– ставка процентов по условиям займа; sn; i – коэффициент наращения финансовой ренты; n– срок долга в годах; i – ставка процентов при создании фонда погашения.
В формуле (6.1) фигурируют две ставки процентов:
1) i – определяет скорость роста суммы фонда погашения;
2) q – сумму выплачиваемых за заем процентов.