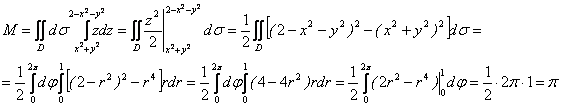Пусть в пространстве XYZ задано тело V. Известно, что масса его задается формулой:
![]() ,
,
где f(P)=f(x, y, z) – плотность.
 Введем прямоугольную сетку с целью выражения бесконечно малого объема dv, разбив тело V системой параллельных плоскостей (рис. 1.19), получим:
Введем прямоугольную сетку с целью выражения бесконечно малого объема dv, разбив тело V системой параллельных плоскостей (рис. 1.19), получим:
![]() . (1.61)
. (1.61)
Тройной интеграл теперь записывается так:
![]() (1.62)
(1.62)
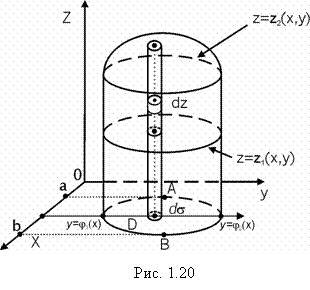 Чтобы свести тройной интеграл к трехкратному (повторному), поступаем так, как это было изложено для двойного интеграла. Предположим, что тело V ограничено поверхностями z = z1(x, y) – снизу и z = z2(x, y) – сверху и цилиндрической поверхностью с боков (её может не быть). Функции z1(x, y) и z2(x, y) заданы в области D – проекции тела V на плоскость оси xОz. Каждая прямая, параллельная оси Оz и проходящая через внутреннюю точку D, пересекает границу V в двух точках – точке входа на z = z1(x, y) и точке выхода на поверхность z = z2(x, y) (рис. 1.20).
Чтобы свести тройной интеграл к трехкратному (повторному), поступаем так, как это было изложено для двойного интеграла. Предположим, что тело V ограничено поверхностями z = z1(x, y) – снизу и z = z2(x, y) – сверху и цилиндрической поверхностью с боков (её может не быть). Функции z1(x, y) и z2(x, y) заданы в области D – проекции тела V на плоскость оси xОz. Каждая прямая, параллельная оси Оz и проходящая через внутреннюю точку D, пересекает границу V в двух точках – точке входа на z = z1(x, y) и точке выхода на поверхность z = z2(x, y) (рис. 1.20).
Возьмем бесконечно малый элемент с высотой dz и проекцией ![]() на плоскость xОy, его масса будет:
на плоскость xОy, его масса будет:
![]() .
.
Чтобы найти массу «столбика» надо «просуммировать» все такие элементы:
![]() .
.
Для определения массы всего тела V, нужно «просуммировать» массы всех «столбиков»:
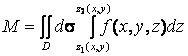 . (1.63)
. (1.63)
Сравнение (1.63) с (1.62) дает формулу:
![]() (1.64)
(1.64)
Методическое руководство
Расстановка пределов обычно проводится в следующем порядке: внешний интеграл имеет постоянные пределы а и b; далее для внутреннего двойного интеграла — от точки входа ![]() до точки выхода
до точки выхода ![]() ; для внутреннего тройного интеграла — от точки входа
; для внутреннего тройного интеграла — от точки входа ![]() до точки выхода.
до точки выхода.
Отметим, что имеет место операция изменения порядка интегрирования. Первым вычисляют внутренний интеграл для тройного, результат подводят под внутренний интеграл для двойного и последним вычисляют обычный определенный интеграл, получают число. Таким образом, тройной интеграл трехкратным интегрированием сводится к определенному интегралу.
Пример 1
Вычислить:
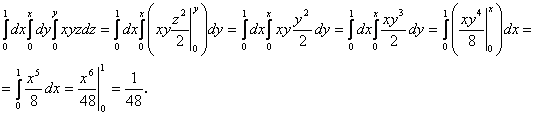
Пример 2
Найти объем тела, ограниченного плоскостями ![]() и
и ![]() (рис. 1.21).
(рис. 1.21).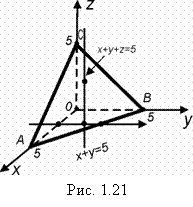
Решение. Согласно формуле (1.46) имеем:
![]() .
.
Тогда, применяя порядок как в (1.64), получим:

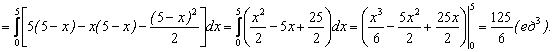
Пример 3
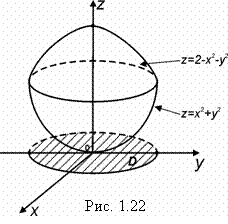 Тело, ограничено поверхностями
Тело, ограничено поверхностями ![]() и
и ![]() . Плотность массы тела в каждой точке равна аппликате точки:
. Плотность массы тела в каждой точке равна аппликате точки: ![]() . Найти массу тела.
. Найти массу тела.
Решение. При вычислении двойного интеграла часто удобно прибегать к полярным координатам. По (1.64) имеем:
![]() .
.
Найдем проекцию D тела V на xОy (рис. 1.22).
Решим совместно уравнения:
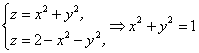 – круг радиуса R = 1.
– круг радиуса R = 1.
Тогда