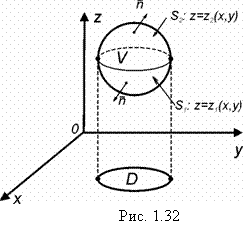
Пусть в замкнутой области V пространства, ограниченной замкнутой поверхностью S, заданы непрерывные функции вместе со своими частными производными первого порядка X, Y, Z(x, y, z). Предположим для простоты, что V ограничено снизу куском S₁ поверхности z = z₁(x, y), а сверху куском S₂ поверхности z = z₂(x, y) (рис. 1.32).

Тогда

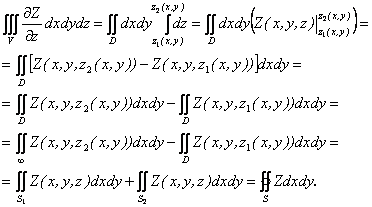
Следовательно,

.                                                  (1.85)

Аналогичным образом можно получить формулы:

;                                                  (1.86)

.                                                   (1.87)

Сложим почленно (1.85) – (1.87), получим формулу Остроградского:

                     (1.88)

(нормаль внешняя).

Пример 1

Преобразовать по формуле Остроградского поверхностный интеграл:

в тройной.

Решение. По формуле (1.88) имеем:

,

где       V – замкнутая область, ограниченная замкнутой поверхностью S.

Пример 2

Используя формулу Остроградского найти

,

где       S – сфера , ограничивающая шар V.

Решение. По формуле (1.88) имеем:

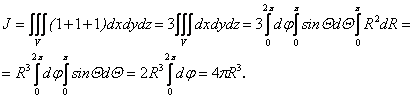
Пример 3

С помощью формулы Остроградского найти формулу для вычисления объема тела V.

Решение.

Но                                               ;  ; 

тогда, когда X,Y,Z являются линейными функциями с одним и тем же коэффициентом пропорциональности:

Следовательно,

Отсюда

Окончательно:

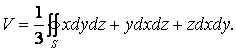                                    (1.89)

Формула (1.89) дает повод на установление других формул, позволяющих через поверхностный интеграл находить объемы тел. Как упражнения: получите другие формулы для вычисления объёмов тел через поверхностные интегралы.