Областью в комплексной плоскости называется множество D точек этой плоскости, обладающее свойствами:
1) открытости – вместе с точкой из D этому множеству принадлежит и достаточно малая окрестность с центром в этой точке;
2) связности – любые две точки D можно соединить ломаной, целиком состоящей из точек D.
Примером области могут служить окрестности точек на комплексной плоскости. Под e-окрестностью точки z0 понимают открытый круг радиуса e с центром в этой точке: |z – z0| < e.
Область называется ограниченной (или конечной), если все ее точки можно поместить в круг достаточно большого конечного радиуса R. В противном случае область называется неограниченной (бесконечной).
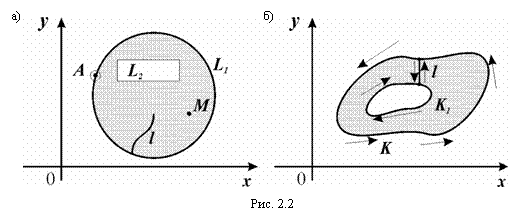
Граничной точкой области D называют такую, которая сама не принадлежит D, но в любой ее окрестности лежат точки этой области (рис. 2.2,а). Совокупность граничных точек области D называется границей этой области.
 Например, для e-окрестности точки z = i является окружность |z–i|=e. Так как z = x+iy, то |x + iy –i| = e Þ
Например, для e-окрестности точки z = i является окружность |z–i|=e. Так как z = x+iy, то |x + iy –i| = e Þ ![]() = e Þ x2 + (y – 1)2 = e2 – окружность радиуса e с центром в точке х = 0, у = 1 комплексной плоскости.
= e Þ x2 + (y – 1)2 = e2 – окружность радиуса e с центром в точке х = 0, у = 1 комплексной плоскости.
Область с присоединенной к ней границей называют замкнутой и обозначают D. Будем в дальнейшем предполагать, что граница области состоит из конечного числа замкнутых линий, разрезов (дуг) и точек. Линии и разрезы, входящие в состав границы будем предполагать всегда кусочно-гладкими.
Область называется односвязной, если граница состоит из одной связной линии. Область называется многосвязной, если граница области состоит из нескольких связных частей, например: двухсвязной, трехсвязной и т.д. – по числу не связных между собой частей границы. На рис. 2.2,б – пример двухсвязной области.
Обход односвязной области считается положительным, если она остается по левую руку (контур обходится против хода часовой стрелки). На рис. 2.2,б сделан разрез l, а обход области изображен положительным (область в результате разреза стала односвязной).
Пример 1
Построить области:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или неограниченной, односвязной или многосвязной.
Решение:
а) ![]() поэтому получим:
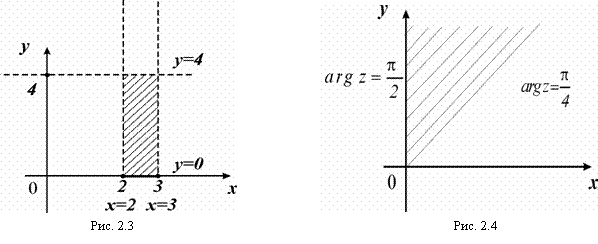
поэтому получим: ![]() . Область (рис. 2.3) – замкнутая, ограниченная, односвязная.
. Область (рис. 2.3) – замкнутая, ограниченная, односвязная.
 б)
б) ![]() и
и ![]() – лучи, выходящие из начала координат (рис. 2.4). Все точки, удовлетворяющие неравенству б) лежат внутри угла, образованного этими лучами, и на сторонах этого угла. Следовательно, область замкнутая, неограниченная, односвязная.
– лучи, выходящие из начала координат (рис. 2.4). Все точки, удовлетворяющие неравенству б) лежат внутри угла, образованного этими лучами, и на сторонах этого угла. Следовательно, область замкнутая, неограниченная, односвязная.
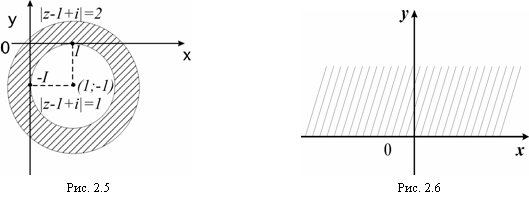
Неравенство ![]() означает, что расстояние каждой точки z от точки
означает, что расстояние каждой точки z от точки ![]() больше 1, но меньше 2. Поэтому областью есть кольцо (его внутренность), ограниченное концентрическими окружностями с центром в точке
больше 1, но меньше 2. Поэтому областью есть кольцо (его внутренность), ограниченное концентрическими окружностями с центром в точке ![]() . Область – открытая, ограниченная, двухсвязная (рис. 2.5).
. Область – открытая, ограниченная, двухсвязная (рис. 2.5).
г) Неравенство ![]() равносильно
равносильно ![]() или
или
![]() ,
,
или, возведя в квадрат обе части, получим:
х2 + у2 – 2у + 1 < х2 + у2 + 2у + 1.
Отсюда: ![]() – верхняя полуплоскость (рис. 2.6).
– верхняя полуплоскость (рис. 2.6).
Вывод: область у>0 – открытая, неограниченная, односвязная (рис. 2.4).
Определение. Кривая называется непрерывной, если она может быть задана параметрическими уравнениями:
![]() , (2.18)
, (2.18)
в которых ![]() – непрерывные функции на отрезке
– непрерывные функции на отрезке ![]() .
.
Например, окружность ![]() ; дуга окружности
; дуга окружности
![]() ; дуга параболы
; дуга параболы ![]() – непрерывные кривые; гипербола
– непрерывные кривые; гипербола ![]() не является непрерывной, так как функции эти при
не является непрерывной, так как функции эти при ![]() и
и ![]() имеют точки разрыва.
имеют точки разрыва.
С помощью комплексного переменного ![]() параметрические уравнения кривой (2.18) можно записать в виде одного уравнения:
параметрические уравнения кривой (2.18) можно записать в виде одного уравнения:
![]() . (2.19)
. (2.19)
Например, уравнение эллипса с полуосями a и b можно записать:
![]() ;
;
уравнение окружности радиуса R
![]() ;
;
единичной окружности:
![]() ;
;
уравнение окружности ![]() с центром в точке
с центром в точке ![]() запишется так:
запишется так:
![]() .
.
Задачи для упражнений
1) Построить в комплексной плоскости линии, точки которых удовлетворяют уравнениям:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д) ![]() е)
е) ![]() ж)
ж) ![]() ; з)
; з) ![]()
2) Построить на комплексной плоскости z области, заданные условиями:
а) ![]() б)
б) ![]() в )
в ) ![]()
г) ![]() д)
д) ![]()
Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или нет, односвязной или многосвязной.
3) Какие кривые определяются следующими уравнениями:
а) ![]() б)
б) ![]() в)
в) ![]() ;
;
г) ![]() д)
д) ![]() е)
е) ![]()
ж) ![]() .
.
Ответы: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д) ![]()
е) ![]() ж)
ж) ![]()