Определение. Если каждому комплексному числу  поставлено в соответствие одно или несколько комплексных чисел , то говорят, что  есть функция от z и пишут:

.                                                                (2.20)

Здесь: D – область определения, а Q – область значений функции. Функция называется однозначной, если каждому  поставлено одно число , в противном случае – многозначной. Например:

а) функция  определена на всей комплексной плоскости и однозначная;

б) функция  определена для всех , однозначная;

в)  определена на всей плоскости хОу и двузначная, так как квадратный корень имеет два значения;

г) целая рациональная функция  – есть однозначная функция, заданная на всей комплексной плоскости;

д) дробно-рациональная функция  – однозначная функция, определена на всей плоскости, из неё выброшены точки, в которых знаменатель равен нулю. Например,  – однозначная функция, определена для всех z;    – однозначная и определена на всей плоскости, кроме точек ;

е) иррациональные функции многозначны.

Так как , где х и у вещественные, задание числа  требует двух вещественных чисел u и v, поэтому задание функции комплексного переменного  равносильно заданию двух функций двух действительных переменных х и у:

.

Например, если , то

.

Вывод: если

.                  (2.21)

График  нельзя наглядно представить, так как нужно иметь четырехмерное пространство х, у, u, v четырех действительных переменных. Однако условимся значения аргумента  изображать с помощью точек плоскости хОу, а значения функции  с помощью точек другой плоскости uОv (рис. 2.7).

Тогда функцию комплексного переменного можно геометрически трактовать как отображение одного множества точек из плоскости z на другое множество точек плоскости w (функция считается однозначной). Если функция w однозначная, то такое отображение называется взаимно однозначным (одному z соответствует одно w и наоборот).

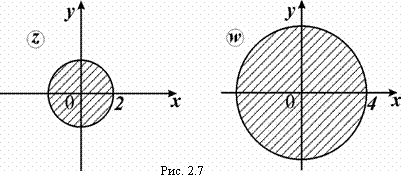
Например, функция  отображает область  из плоскости   на область  плоскости uОv (рис. 2.7). Так как множество точек определено , то поскольку , неравенство  равносильно неравенству .

Отображение кривой. Если в плоскости  кривая К задана уравнением

,                                                        (2.22)

то для того, чтобы найти уравнение отображения (образа) этой кривой К в плоскости w, осуществляемого функцией , достаточно исключить х и у из уравнений (2.21) и (2.22).

Если кривая К задается в параметрическом виде:

x = x(t);    y = y(t),

то, подставляя  и  в (2.22), получим уравнение кривой К также в параметрическом виде:

.                               (2.23)

Пример 1

Найти уравнение линий плоскости w, на которые с помощью функции  отображаются прямые, параллельные мнимой оси:  .

Решение. Чтобы найти образы прямых х = с, подставим вместо х его значение с:

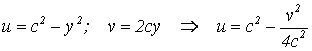 (исключили у).

Получили уравнение семейства парабол, симметричных относительно Оu  (рис. 2.8).

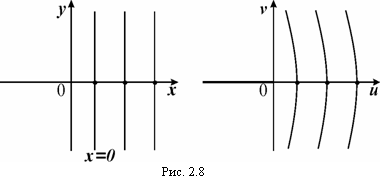Мнимая ось Оу (х = 0) отобразится на линию на плоскости  

,

т.е. имеем луч – отрицательную часть действительной оси  Оu.

В какое семейство отобразятся линии:  и семейство прямых, параллельных действительной оси Ох?

Пример 2

Используя результат примера 1, выяснить, во что перейдет полоса, параллельная оси Оу, лежащая между прямыми х = 1  и  х = 2.

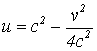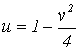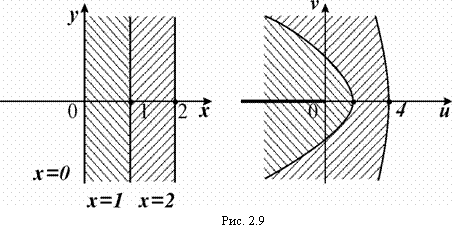
Решение. Полосу можно представить как в процессе «заметания» прямой х = с, когда с изменяется от 1 до 2. При этом парабола  «заметет» криволинейную полосу между параболами  и 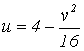 (рис. 2.9). Если взять полосу между х = 0  и

х = 1, то таким же образом, при измении  с = 1 до  с = 0  эта полоса отобразится в область, «заметаемую» параболой  когда параметр с изменяется от 1 до 0, т.е. расположенную между параболой   и   (см. рис. 2.9). Парабола  при с ® 0   вырождается в дважды пробегаемую отрицательную часть оси Оu. Заметим, что

поскольку ограниченные прямые х = 0  и  х = 1  в полосу не включаются, то и их образы ,  , т.е. отрицательная часть оси Оu не должны включаться в образ полосы (рис. 2.9, жирные линии на плоскости w). Говорят так: полоса отобразилась с помощью  на внутреннюю часть параболы  с разрезом вдоль отрицательной части действительной оси.

Пример 3

В какую область функция  отображает первый квадрант  ?

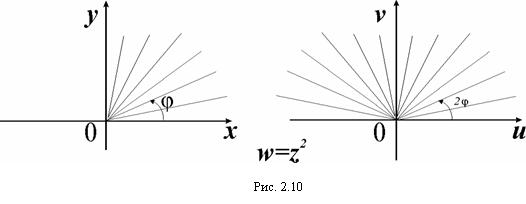
Решение. Функция  отображает луч, выходящий из начала координат, в луч, так как точка  опишет луч, если , а. Но . Откуда видно, что аргумент w равен 2j, т.е. вдвое больше, чем для z, а модуль  и также изменяется от 0 до ¥. Значит, точка w опишет луч, с углом наклона 2j (рис. 2.10).

В какую область функция  отображает верхнюю полуплоскость ?

В какую область функция  отображает угол  на плоскости w?