Будем предполагать, что функция ![]() определена и однозначная в окрестности точки
определена и однозначная в окрестности точки ![]() , кроме, возможно, самой точки
, кроме, возможно, самой точки ![]() .
.
Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , если
, если ![]() , удовлетворяющих
, удовлетворяющих ![]() , выполняется неравенство
, выполняется неравенство ![]() . Записывают:
. Записывают:
![]() .
.
Этот факт геометрически можно истолковать так: модуль разности двух комплексных чисел дает расстояние между точками, их изображающими, когда в плоскости z приближается к точке ![]() так, что расстояние между ними стремится к нулю, а в плоскости функции w бесконечно приближается к точке
так, что расстояние между ними стремится к нулю, а в плоскости функции w бесконечно приближается к точке ![]() . Можно дать и другое истолкование: неравенство
. Можно дать и другое истолкование: неравенство ![]() выражает
выражает ![]() -окрестность точки
-окрестность точки ![]() (круг радиуса
(круг радиуса ![]() ), а
), а ![]() – окрестность точки
– окрестность точки ![]() (круг радиуса
(круг радиуса ![]() );
); ![]() задается, а
задается, а ![]() определяется по
определяется по ![]() : число
: число ![]() есть предел функции
есть предел функции ![]() при
при ![]() , если для всякой
, если для всякой ![]() -окрестности точки
-окрестности точки ![]() , можно найти
, можно найти ![]() - окрестность точки
- окрестность точки ![]() , то для всех точек z этой окрестности (кроме, возможно, самой точки
, то для всех точек z этой окрестности (кроме, возможно, самой точки ![]() ) соответствующие значения
) соответствующие значения ![]() будут изображаться точками
будут изображаться точками ![]() -окрестности точки
-окрестности точки ![]() .
.
Данное определение предела функции формально ничем не отличается от определения предела функции действительного аргумента. Следовательно, все доказанные теоремы математического анализа о пределах остаются в силе для ТФКП. Однако следует отметить важное отличие в определении предела для комплексного переменного – это стремление ![]() происходит по любому пути в окрестности (и за пределами) к точке
происходит по любому пути в окрестности (и за пределами) к точке ![]() . Это весьма существенно, и в дальнейшем используется в разных ситуациях.
. Это весьма существенно, и в дальнейшем используется в разных ситуациях.
Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если она определена в точке
, если она определена в точке ![]() и ее окрестности, и
и ее окрестности, и
![]() . (2.24)
. (2.24)
Функция называется непрерывной в области ![]() , если она непрерывна в каждой точке этой области. Очевидно, что для непрерывности функции
, если она непрерывна в каждой точке этой области. Очевидно, что для непрерывности функции ![]() необходимо и достаточно, чтобы были непрерывными в точке
необходимо и достаточно, чтобы были непрерывными в точке ![]() , функции u(x0,y0) и v(x0,y0).
, функции u(x0,y0) и v(x0,y0).
Отметим без доказательства, что для функций, непрерывных в замкнутых областях, остаются справедливыми свойства функций вещественного переменного. Именно: каждая функция ![]() , непрерывная в замкнутой области
, непрерывная в замкнутой области ![]() :
:
1) ограничена в ![]() , т.е.
, т.е. ![]() , что
, что ![]() ;
;
2) ![]() , где
, где ![]() – соответственно наименьшее и наибольшее значение модуля функции.
– соответственно наименьшее и наибольшее значение модуля функции.
Приращение функции ![]() есть:
есть:
![]() , (2.25)
, (2.25)
где ![]() – приращение аргумента.
– приращение аргумента.
Производная от функции ![]() формально находится так же, как это установлено в математическом анализе, а именно:
формально находится так же, как это установлено в математическом анализе, а именно:
![]() (2.26)
(2.26)
(понятие производной вводится для однозначной функции). Отметим, что все свойства и теоремы, аналогичные вещественному переменному, имеют место и для ТФКП. Иной смысл имеет толкование ![]() и
и ![]() .
.
Пусть существует ![]() . Расположим плоскости z и w так, чтобы действительные и мнимые оси соответственно были параллельны (рис. 2.11).
. Расположим плоскости z и w так, чтобы действительные и мнимые оси соответственно были параллельны (рис. 2.11).
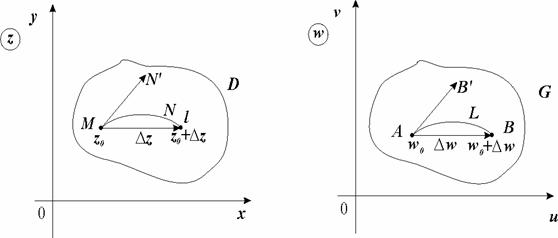
Рис. 2.11
Рассмотрим в плоскости z две точки ![]() и кривую
и кривую ![]() , проходящую через них. Этим точкам в плоскости w будут соответствовать точки
, проходящую через них. Этим точкам в плоскости w будут соответствовать точки ![]() и кривая L. Вектору
и кривая L. Вектору ![]() будет соответствовать вектор
будет соответствовать вектор ![]() . Известно, что
. Известно, что
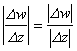 .
.
Переходя к пределу, получим:
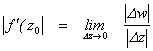 . (2.27)
. (2.27)
Величина ![]() указывает, в каком отношении изменяются линейные размеры при отображении функцией
указывает, в каком отношении изменяются линейные размеры при отображении функцией ![]() . Согласно (2.27) величину
. Согласно (2.27) величину ![]() называют коэффициентом растяжения (
называют коэффициентом растяжения (![]() ) или сжатия (
) или сжатия (![]() ) в точке
) в точке ![]() при отображении области D на G, осуществляемом функцией
при отображении области D на G, осуществляемом функцией ![]() . Обозначают
. Обозначают ![]() =р. В этом состоит геометрический смысл
=р. В этом состоит геометрический смысл ![]() .
.
Для установления геометрического смысла аргумента производной используем известный факт:
![]() .
.
Имеем
![]() . (2.28)
. (2.28)
Но ![]() – угол вектора
– угол вектора ![]() с осью ох, а
с осью ох, а ![]() – угол вектора
– угол вектора ![]() с осью ou. Следовательно, разность между аргументами дает угол между векторами
с осью ou. Следовательно, разность между аргументами дает угол между векторами ![]() и
и ![]() .
.
Если перейти к пределу при ![]() , то секущие
, то секущие ![]() и
и ![]() будут стремиться к положению касательных
будут стремиться к положению касательных ![]() и
и ![]() (рис. 2.11), тогда
(рис. 2.11), тогда
![]()
будет равен углу между касательными ![]() и
и ![]() .
.
Поэтому любая линия (так как направление линии выбрано произвольно), проходящая через точку ![]() , поворачивается при отображении
, поворачивается при отображении ![]() на один и тот же угол, равный аргументу производной, т.е.
на один и тот же угол, равный аргументу производной, т.е. ![]() . В этом состоит геометрический смысл аргумента
. В этом состоит геометрический смысл аргумента ![]() .
.