Рассмотрим некоторые элементарные функции. Важной является целая степенная функция 
, где n > 1. Эта функция целая, так как для любого z(z ¹ 0) существует производная 
. Эта производная отлична от нуля при z¹0. Функция отображает расширенную z-плоскость на расширенную w-плоскость: так как z = 0 и z = ¥ переходят в w = 0 и w = ¥. Всякая точка w, отличная от нуля и бесконечности, имеет ровно n различных корней 
, содержащихся в формуле (2.13)
Следовательно, отображение 
(n > 1) не является взаимно однозначным. К степенной функции прибегают каждый раз, когда нужно отобразить угол на угол раствором в n раз больше первого.
Пример 1
Отобразить взаимно однозначно и конформно внутренность угла D: 
на первую полуплоскость.
Решение: Так как D – угол раствора 
, а верхняя полуплоскость имеет угол раствора 
, то применим два последовательных отображения: 
, которое переводит D в полуплоскость D1: 
. Повернем D1 на угол 
в положительном направлении, т.е. положим 
. Окончательно получим полуплоскость Jm w > 0. Итак искомое отображение: w = iz2.
Показательную и тригонометрические функции: ez, sin z, cos z в случае комплексных значений z Эйлер определил следующим образом.
Определение: Функции ez, sin z, cos z для всякого комплексного z определяются рядами:
; (2.38)
; (2.39)
(2.40)
Эти функции аналитические во всей плоскости. Для упражнения примените признак Даламбера сходимости рядов, убедитесь, что эти ряды сходятся для любого z, т.е. радиус сходимости рядов R=¥. Чтобы сделать вывод об аналитичности названных функций докажем теорему: сумма степенного ряда есть функция аналитическая внутри круга сходимости, причем производную ее можно найти почленным дифференцированием ряда.
Доказательство: Заметим, что сумма степенного ряда
(2.41)
есть однозначная функция для |z|<R. Проверим выполнение условий Даламбера-Эйлера.
Для чего положим 
, n = 0, 1,…, z = r (cosj + isinj).
Тогда
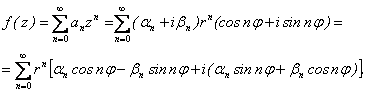
Отсюда:
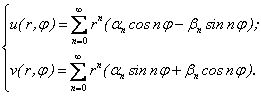(2.42)
Как известно [8], что условия существования производной в случае полярных координат имеют вид:
(2.43)
где f(z) = u(r,j) + iv(r,j), а
. (2.44)
Так,
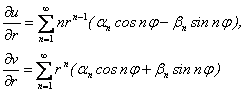(2.45)
Видно, что условие 
выполняется. Второе условие рекомендуется проверить самостоятельно.
Полученные ряды (2.45) равномерно сходятся по признаку Вейерштрасса.
С помощью формулы (2.44) легко вычислить производную (подставив значения 
и 
):
.
Следовательно, f(z) – функция аналитическая внутри круга сходимости на всей комплексной плоскости (R = ¥).
Согласно доказанной теореме производные находятся почленным дифференцированием:
Свойства умножения степеней сохраняются (как было в вещественном анализе). Так, для любых количеств комплексных z1 и z2
. (2.46)
По определению:
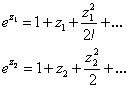
Ряды эти, как степенные, внутри круга сходимости сходятся абсолютно, значит, их можно перемножать:
.
Из формулы Эйлера следуют равенства:
. (2.47)
С помощью формулы Эйлера и правила умножения степеней проверяются известные тригонометрические формулы, которые верны и для комплексных z. Например:
;
.
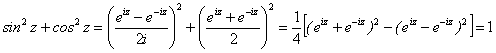Гиперболические функции вводятся по определению:
. (2.48)
Легко устанавливается связь между тригонометрическими и гиперболическими функциями. Имеем:
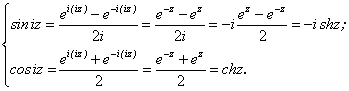(2.49)
Методическое руководство
При вычислении значений 
, sin z, cos z, sh z, ch z для любого z использование рядов нецелесообразно.
Пример 2
Пример 3
Функция ez в области комплексного переменного обладает новым свойством, а именно: функция ez – периодическая с периодом 2pi.
В самом деле,
.
Показательная функция – функция аналитическая во всей плоскости z. Так:
.
Отсюда
.
Условия Даламбера-Эйлера выполняются (проверьте) всюду на плоскости z. Так как нигде 
, то отображение, осуществляемое показательной функцией, конформно во всей плоскости z.
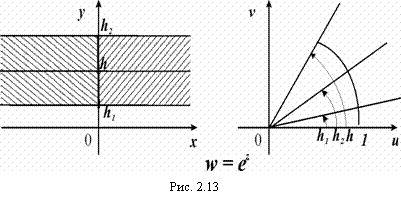
Покажем, что w = ez точки прямой y = h, параллельной оси Ох, взаимно однозначно отображются в точки луча, выходящего из начала координат под углом h к положительному направлению действительной оси (рис. 2.13).
Так, если y = h, то z = x + iy, причем вдоль y = h абсцисса х изменяется от -¥ до +¥. Значит, 
. Отсюда делаем вывод, что arg w = h остается постоянным, а |w| = ex изменяется от e-¥ до e+¥, т.е. от 0 до ¥. Итак, когда z описывает прямую y = h, то w описывает луч arg w = h. Если в плоскости z взять полосу, параллельную оси х то y = h1 до y = h2.
Функция w = ex эту полосу шириной h £ 2p, конформно отображает в угол с вершиной в начале координат раствора h (h1< arg w < h2). В частности, полоса шириной p отображается в полуплоскость, а полоса шириной 2p – в плоскость с разрезом вдоль луча arg w = h1 . (рис. 2.14).
 |
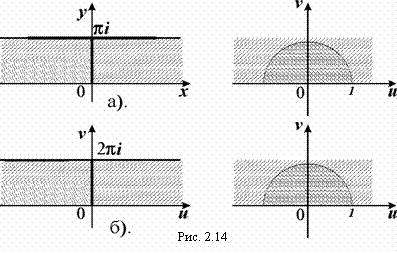Определив показательную функцию, теперь легко дать определение логарифмической функции. Она определяется как функция, обратная показательной: число w называется логарифмом числа z, если 
и обозначается:
w = Ln z.
Найдем действительную и мнимую части логарифмической функции w = u + iv, z = x + iy. По определению:
.
Перейдем к показательной форме, получим:
,
откуда
1) 
2) 
Тем самым, получили формулу для логарифмической функции
Ln z = ln r+i(arg z + 2kp). (2.50)
Из (2.50) видно, что логарифмическая функция определена во всей плоскости z, кроме z = 0 и является многозначной (k = 0, ±1,…).
Беря главное значение аргумента (k=0), получают однозначную ветвь логарифмической функции и обозначают:
Ln z = ln |z|+i arg z. (2.51)
Пример 1
Найти общее и главное значение логарифмов чисел:
а) -5; б) 4i; в) 1+i; г) e.
Решение:
а) число -5 представим в тригонометрической форме: z = |-5| = 5;
arg(-5) = p, следовательно по формуле (2.50): Ln(-5) = ln5 + i(p + 2kp);
ln(-5) = ln5 + ip.
б) число 4i представим в тригонометрической форме: r = |4i| = 4; 
, тогда как и ранее 
в) число 1+i: 
.
г) число е – вещественное, поэтому |e| = e, arg e = 0 и
Ln e = ln e + i(0 + 2kp) = 1 + 2kp i; ln e = 1.
Логарифмическая функция в смысле главного значения – аналитическая во всей плоскости z, кроме точки z =0 и z = ¥, а в плоскости с разрезом, соединяющим точки z = 0 и z = ¥, распадается на бесконечное число регулярных ветвей.
Пример 2
Пусть D0 – плоскость z с разрезом по лучу (0; ¥). В этой области w = ln z распадается на регулярные ветви:
(ln z)k = ln|z| + i(arg z) k + 2kp i, k = 0, ±1,…,
где 0 < (arg z) < 2p. Функция w = (ln z)k конформно отображает D0 на полосу 2kp < Jm w < 2(k+1) p.
Пример 3
Во что отображает функция w = ln z плоскость с разрезом (-¥; 0) – вдоль отрицательной действительной оси?
 |
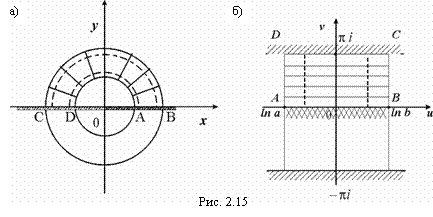Решение: Так как 
, то согласно определению функции, как обратной к показательной, функция w = ln z взаимно однозначно отображает плоскость с разрезом (-¥; 0) на полосу -p < v < p (рис. 2.15).
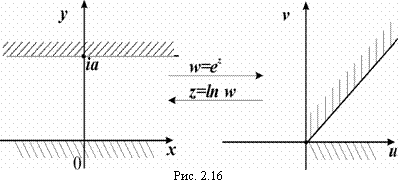
Пример 4
Сектор 0 < arg z < a£ 2p отобразить с помощью функции w = ln z из плоскости z на плоскость w.
Решение: Функция w = ez взаимно однозначно и конформно отображает полосу 0 < Jm z < a ширины a < 2p на сектор: 0 < arg z < a. Следовательно, обратная функция z = ln w взаимно однозначно и конформно отображает сектор 0 < arg z < a на полосу 0 < Jm z<a (рис. 2.16).
Изучив логарифмическую функцию, можно ввести понятие степени комплексного числа с комплексным показателем. По определению логарифмической функции имеет место равенство:
(2.52)
для любого комплексного 
.
Следовательно, равенство
(2.53)
справедливо для любых комплексных и z.
В силу многозначности логарифма 
– многозначно. Его главным значением считаем то, которое соответствует 
.
Пример 5
Вычислить: а) 
; б) 21+i;
а) 
.
б) 
(k = 0, 
1,…)
Задачи для упражнений
1) Найти:
а) 
; б) 
; в) 
; г) 
; д) 
; е) 
; ж) 
;
з) 
; и) 
; к) 
; л) 
; м) 
.
Ответы: а) i; б) –ei; в) 
; г) 
; д) 
;
е) 
; ж) 
; з) 
; и) 
к) 
; л) 
; м) 
.
2) Доказать тождества:
а) 
;
б) 
.
3) Убедиться, что для функций w = cos2z и w = shz выполняются условия Даламбера-Эйлера.
В курсе ТФКП и ее приложениях встречаются задачи, использующие обратные гиперболические функции [9]. Поэтому дадим возможность усвоения процесса перехода на двух примерах.
Пусть требуется получить выражение для обратной тригонометрической функции w = arcsin z. Эта функция определяется как функция, обратная к функции z =sin w. Последняя выражается через показательные, поэтому следует ожидать, что обратная тригонометрическая функция выражается через логарифмы:
,
откуда
.
Решив это квадратное уравнение относительно 
, получим:
откуда
;
. (2.54)
Аналогично получим, если 
(читается: «ареа»), т.е.
, откуда 
.