Теорема, о которой будет идти речь далее играет фундаментальную роль в ТФКП и многих её приложениях.

Теорема Коши: интеграл по замкнутой кривой К равен нулю, если кривая ограничивает односвязную область D, а подынтегральная функция аналитическая не только внутри этой области, но и в области D’, содержащей D и её границу К:

.                                                           (2.67)

Доказательство. Применим формулу Грина из анализа:

,

где D  -область, ограниченная кривой K к обоим интегралам, стоящим в (2.58), получим:

,

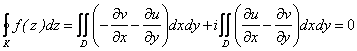так как для w = f(z) имеют место условия Даламбера-Эйлера.

Пример 1

, по любой замкнутой кривой, так как функция z²-5z – аналитическая во всей z плоскости.

Пример 2

, если К ограничивает область, не содержащую особых точек функции  ни внутри, ни на границе К. Для их нахождения приравняем к нулю, знаменатель:  – особые точки.

Тогда, если К – окружность |z + 3| = 1, то интеграл равен 0; если К: |z| = 0,1, то теорему Коши применить нельзя (так как точка z = 0 лежит в круге |z| < 0,1).

Решая примеры на вычисления интегралов, приходим к вопросу: при каком условии интеграл не зависит от пути интегрирования? На поставленный вопрос ответ дает основная теорема Коши, которую формулируют так:

Если в односвязной области D функция f(z) аналитическая, то для всех кусочно-гладких кривых К, лежащих в этой области и имеющих общие концы, интеграл  имеет одно и то же значение, т.е. интеграл от формы пути не зависит.

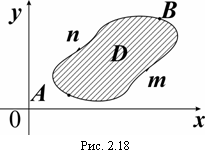По основной теореме Коши  и свойству аддитивности имеем (рис. 2.18):

так как путь AnB проходит в противоположном направлении и по свойству (2.63) интеграл дает противоположное значение.