Изучая теорию рядов в математическом анализе, получили определения рядов с комплексными членами, степенных рядов, круга и радиуса сходимости и нахождение радиуса по формуле Коши-Адамара:

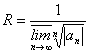.                                                           (2.90)

Таким образом, в ТФКП степенной ряд имеет вид:

                            (2.91)

где z₀,, a_n (n = 0, 1, 2…) – фиксированные комплексные числа, а z – комплексная переменная.

Областью сходимости ряда (2.91) является круг сходимости с центром в точке z₀ радиуса R, который находят по формуле (2.90).

В круге сходимости  степенного ряда сумма его  есть аналитическая функция, причем производная может быть получена почленным дифференцированием ряда:

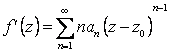,                                                  (2.92)

Если применить этот процесс к сумме ряда (2.92), то видим, что  – аналитическая в круге  и

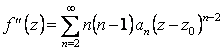.                                          (2.93)

Следовательно, сумма степенного ряда (2.91) бесконечно дифференцируема в круге , а

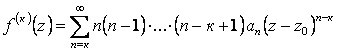.                            (2.94)

Если в (2.94) положить z = z₀, то найдем:

                                            (2.95)

откуда 

,                                                           (2.96)

(считаем ).

Степенной ряд (2.91) можно теперь записать в виде:

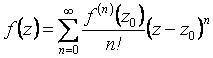.                                        (2.97)

Ряд (2.97) называется рядом Тейлора для .

Вывод: каждый степенной ряд с R > 0 является рядом Тейлора для своей суммы.