Используя интегральную формулу Коши, покажем, что всякую аналитическую функцию в круге сходимости можно представить в виде суммы степенного ряда.

Теорема. Пусть функция  – аналитическая в области D. Если   и R – расстояние z₀ до границы области D, то в круге  она разлагается в ряд Тейлора.

Пусть ; рассмотрим круг  (рис. 2.27).

Если К_r1– граница круга, то

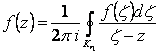.                      (2.98)

Разложим  в ряд по степеням z-z₀:

,

тогда

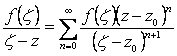.                                           (2.99)

При фиксированном z ряд (2.99) равномерно сходится относительно , так как

,

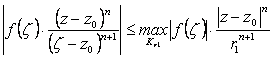а мажорантный ряд  также сходится. Следовательно, ряд (2.99) можно интегрировать почленно:

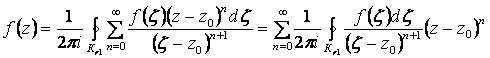.          (2.100)

Из (2.100) видно, что коэффициенты ряда

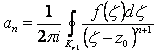                                              (2.101)

и не зависят от контура интегрирования. Поэтому интеграл в (2.101) берут по контуру К_r.

Вывод: показали, что f(z) является суммой степенного ряда (Тейлора) в круге :

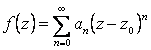
с коэффициентами:

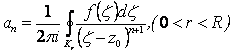.                                     (2.102)

Методическое руководство

1) Если известны особые точки , то радиус сходимости ряда Тейлора можно найти так. Особые точки функции являются граничными для области ее аналитичности. Согласно теореме радиус сходимости ряда Тейлора не меньше, чем расстояние от точки z₀ до ближайшей особой точки функции.

2) Имеет место свойство единственности разложения функции в ряд Тейлора. Это значит, что каким бы методом мы ни разлагали функцию в ряд Тейлора он единственный. Поэтому коэффициенты  не обязательно находить по формуле (2.102).

Пример 1

Найти первые три члена разложения функции  по степеням z + i и определить радиус сходимости ряда.

Решение. По условию должны записать ряд (z₀ = – i):

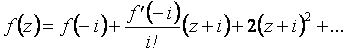
Найдем последовательно

;

.

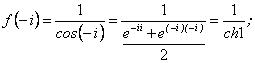
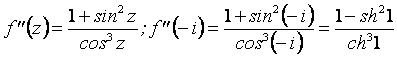Тогда

.

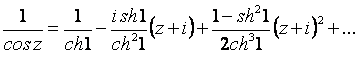Найдем особые точки данной функции, для чего знаменатель приравняем нулю (cos z = 0).

Отсюда  – особые точки. 

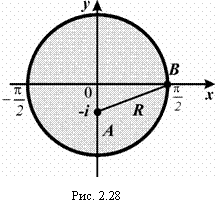
Для нахождения радиуса сходимости определим расстояние от точки  -i до ближайшей особой точки (их две)  (рис. 2.28). По теореме Пифагора:

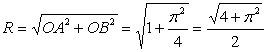 – радиус сходимости ряда.

Пример 2

Разложить в ряд Тейлора функцию в окрестности точки z=0, не находя коэффициентов с помощью производных и применения формул (2.102)

Решение. Согласно свойства единственности, разложим cos z в ряд Маклорена и, проведя указанные действия, получим:

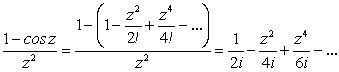
Задачи для упражнений

1) Найти три первых не равных нулю члена разложения функции  по степеням  и определить радиус сходимости ряда.

Ответ:

2) Найти несколько первых членов разложения по степеням z функции  и определить радиус сходимости ряда.

Ответ: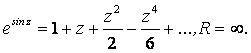  

3) Разложить в ряд Тейлора по степеням  функцию .

Ответ:   .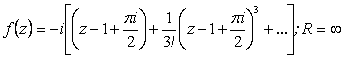

4) Разложить в ряд Тейлора по отношениям z функцию .

Ответ:   .

5) Разложить в ряд Тейлора функцию  в окрестности точки z₀ = 0 (N = 1, 2,…) для N = 3.

Ответ:   .