Применение формулы (3.1) непосредственно бывает весьма громоздко. Теоремы, которые рассмотрим далее, значительно облегчают решение задачи нахождения изображений большого числа разнообразных функций. Важно то, что они облегчают решать также обратную задачу – отыскания оригиналов по изображениям.
1) Теорема о дифференцировании изображения
Если ![]()
![]()
![]()
![]()
![]() .
.
Доказательство. Функция ![]() . Применим (3.1), получим:
. Применим (3.1), получим:
![]()
![]()
![]()
![]() .
.
Итак,
![]()
![]()
![]() . (3.28)
. (3.28)
Методическое руководство
Умножение оригинала на независимую переменную влечет в области изображений взятие производной по переменной p с последующим умножением результата на минус единицу.
Поэтому, умножив ![]() на t, в результате получим:
на t, в результате получим:
![]()
![]()
![]() .
.
Продолжая этот процесс, получим:
![]()
![]()
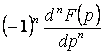 . (3.29)
. (3.29)
Пример 1
Найти изображение ![]() .
.
Решение. Так как ![]()
![]()
![]() , то по (1.4.7) получим:
, то по (1.4.7) получим:
![]()
![]()
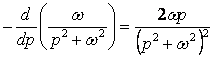 .
.
2) Теорема умножения (Э. Бореля) (теорема о свертке):если ![]()
![]()
![]()
![]()
![]() , то
, то
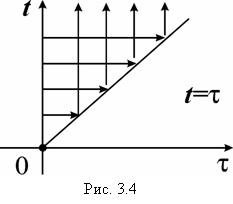
![]()
![]()
![]() . (3.30)
. (3.30)
Интеграл ![]() называется сверткой функций
называется сверткой функций ![]() и
и ![]() и обозначается:
и обозначается: ![]() .
.
Если f1 и f2 – оригиналы, то свертка их является оригиналом. Найдем изображение, применяя (3.1):
![]()
![]()
![]() .
.
Меняя порядок интегрирования (область интегрирования изображена на (рис. 3.4), получим:
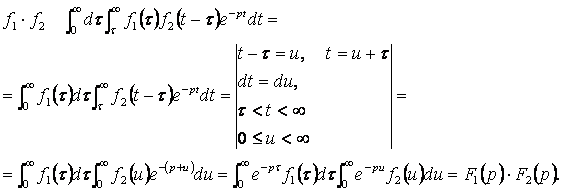
Пример 2
Найти оригинал, если 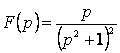 .
.
Решение. Выполним тождественное преобразование, получим:
![]()
![]()
![]()
![]()
![]()
По теореме о свертке найдем:
![]()
![]()
![]() .
.
3) Первая теорема разложения: если F(p) разлагается в степенной ряд по отрицательным степеням p с ненулевым радиусом сходимости, т.е.
![]() , (3.31)
, (3.31)
то оригиналом такой функции также является степенной ряд по положительным степеням t –
![]() (3.32)
(3.32)
который сходится при всех ![]()
![]()
![]()
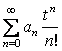 . (3.33)
. (3.33)
Подробное доказательство не станем приводить. Доказательство приводит к утверждению, что ряд (3.32) равномерно сходится при всех t > 0 , и его сумма есть ![]() .
.
4) Вторая теорема разложения: если ![]() правильная несократимая рациональная дробь, знаменатель Q(p) который имеет корни
правильная несократимая рациональная дробь, знаменатель Q(p) который имеет корни ![]() соответственно кратностей
соответственно кратностей ![]() , то оригинал определяется по формуле:
, то оригинал определяется по формуле:
 (3.34)
(3.34)
Доказательство. По формуле обращения (3.1)
![]() . (3.35)
. (3.35)
Учитывая определение вычета относительно кратного полюса, сразу получим доказательство теоремы. Если все корни Q(p) простые (![]() ), то в результате получим:
), то в результате получим:
 (3.36)
(3.36)
Пример 3
Найти оригинал изображения ![]() .
.
Решение. Определим корни знаменателя ![]() :
:
![]() . Корень 0 – третьей кратности, а корни 1 и 2, простые. Для нахождения оригинала используем формулы (3.34) и (3.36). Здесь r1 = 3, r2 = 1, r3 = 1.
. Корень 0 – третьей кратности, а корни 1 и 2, простые. Для нахождения оригинала используем формулы (3.34) и (3.36). Здесь r1 = 3, r2 = 1, r3 = 1.
Следовательно,

Методическое руководство
На практике часто не используют теорию вычетов, а разлагают дробь на сумму простейших, как это делали в интегральном исчислении при интегрировании дробно-рациональных функций.
Решение можно оформлять и по-другому.
Пример 4
Найти оригинал ![]() для изображения
для изображения ![]() .
.
Решение. ![]() – правильная рациональная несократимая дробь, причем
– правильная рациональная несократимая дробь, причем ![]() . Корни знаменателя простые:
. Корни знаменателя простые: ![]() значит можно применить вторую теорему разложения в виде (3.36). Очевидно,
значит можно применить вторую теорему разложения в виде (3.36). Очевидно, ![]() . Все другие действия сведем в таблицу 3.2.
. Все другие действия сведем в таблицу 3.2.
Таблица 3.2
|
|