Пусть имеется однородное тело V, ограниченное поверхностью S. Как известно, температура тела удовлетворяет уравнению:

.

Если процесс установившийся (стационарный), т.е. u(x,y,z) не зависит от времени, то . Следовательно, температура u(x,y,z) удовлетворяет уравнению Лапласа:

                                                                (4.71)

Функции u, удовлетворяющие уравнению Лапласа называются гармоническими (см. главу 2).

Чтобы температура в теле определялась однозначно из уравнения Лапласа, нужно знать температуру на поверхности S. Таким образом, для уравнения Лапласа краевая задача формулируется так: найти функцию u(x,y,z), удовлетворяющую уравнению (4.71) внутри объема V и принимающую в каждой точке  заданные значения:

                                                          (4.72)

Эта задача называется задачей Дирихле или первой краевой задачей для уравнения Лапласа (4.71).

Если рассматривать плоский случай, то уравнению Лапласа должна удовлетворять функция u(x,y), а краевые условия должны иметь место на контуре С, ограничивающем односвязную область D плоскости хОу.

Замечание. В практике часто пользуются уравнением Лапласа, записанного в цилиндрических координатах (полярных, если случай плоский).

Если ввести в рассмотрение цилиндрические координаты:  , то заменяя x, y, z  на r, , z, приходят к функции и^*( r, , z), а уравнение Лапласа этой функции будет иметь вид:

                                     (4.73)

Если функция u не зависит от z, а зависит только от х и у, то функция и^*=и^*( r, ) и удовлетворяет уравнению Лапласа:

                                             (4.74)

Найдём решение задачи Дирихле для круга. Пусть в плоскости Х0У задан круг радиусом R с центром в начале координат и на его окружности задана функция , где  – полярный угол. Требуется найти функцию и( r, ), непрерывную в круге, включая границу, удовлетворяющую внутри круга уравнению Лапласа:

                                                       (4.75)

и на окружности круга принимающую заданные значения:

.                                                   (4.76)

Задачу решаем в полярных координатах. Тогда уравнение (4.75) будет:

или

.                                                 (4.77)

Решение ищем методом разделения переменных, полагая

                                                      (4.78)

Подставляя в уравнение Лапласа, приходим:

                                                 (4.79)

Последнее равенство дает два уравнения:

                                                    (4.80)

                                            (4.81)

Общее решение уравнения (4.80) будет:

                                                  (4.82)

Общее решение уравнения (4.81):

                                                      (4.83)

(решение ищется в форме ).

Запишем решение в виде:

_.                                   (4.84)

Если k = 0, то должны взять  (решение должно быть периодической функцией). Как и ранее решение задачи получим, суммируя все u_k в (4.84), а следовательно, сумма должна быть периодической функцией от , Для этого k должно принимать целые значения (в самом начале мы взяли , а не , так как числу  не отвечало бы периодическим решениям). Функция ограниченна только положительными значениями k = 1, 2,…,n,…, так как в силу произвольности A, B, C, D отрицательные значения k новых частных решений не дают.

Таким образом,

                                 (4.85)

(постоянная C_n включена в А_n и В_n). Подберем А_n и В_n так, чтобы удовлетворить краевое условие (4.76).

Подставив в равенство (4.85) r = R,  получим:

.                                  (4.86)

Отсюда видно, что функция  должна разлагаться в ряд Фурье в интервале  и ,  должны быть коэффициентами Фурье. Следовательно,

.                           (4.87)

Подставляя в формулу (4.85) значения А_n и В_n из (4.87) и проведя тождественные преобразования (рекомендуется выполнить самостоятельно в качестве упражнения), получим:

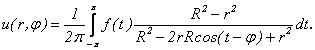                              (4.88)

Формула (4.88) называется интегралом Пуассона. Этим и завершается решение задачи Дирихле для круга.

Пример 1

Показать, что функция  есть гармоническая функция.

Решение. По определению функция u(x,y) называется гармонической в некоторой области, если в каждой точке этой области она удовлетворяет уравнению Лапласа:

Найдем производные u_xx и u_yy. Имеем:

,  

Следовательно,

Вывод: функция  гармоническая.