Задача 1

Проинтерполировать функцию  полиномом , причем совпадение значений  и  требуется при . Найти относительную погрешность приближения   значения.  

Решение

Прежде всего, построим интерполяционную таблицу:

.

x	0	1	2
y	1	2	4

Размерность таблицы равна: 3, ;

.

Получаем систему линейных уравнений:

                              

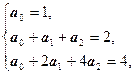
Получаем интерполяционный полином:

.

Проверим результат: ,       ,         ;

 – интерполяционный полином.

Найдём относительную погрешность:

,                         ,

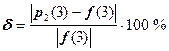f(3) = ,                                                 .

Ответ: ,      .

Задача 2

Проинтерполировать функцию  функцией  ,  причем совпадение значений  и  требуется при x = 0; 1; 2.  Найти относительную погрешность приближения  значения.

Решение

Построим интерполяционную таблицу:

x	0	1	2
y	1	2	4

Для нахождения неизвестных  составим систему уравнений:

                                   

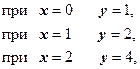
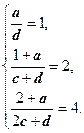
Полагая, что знаменатели дробей не обращаются в нуль, получаем систему линейных уравнений:

Система линейных уравнений имеет единственное решение:

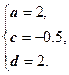
Следовательно,          или      .

Проверим результат:

,              ,               .

Найдём относительную погрешность:

,             ,

.

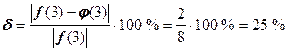Ответ: , .

Отметим, что функция  не является непрерывной при x = 4. В отличие от задачи 1 задача 2 не всегда имеет решение. Существуют интерполяционные таблицы, для которых нельзя построить интерполяционную функцию j(x). В этом случае в ответе нужно указать, что задача не имеет решения.

Задача 3

По интерполяционной таблице построить интерполяционный полином   и представить его в виде суммы полиномов Чебышева. Указать число M такое, что

  для :

x	-1	0	1
y	6	1	2

Решение

Сначала нужно построить  в виде:   . Так как размерность таблицы равна 3,   то             .

Запишем систему линейных уравнений для нахождения  неизвестных :

                  

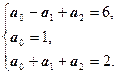
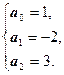
Запишем интерполяционный полином: .

Проверим результат:           ,          ,        .

Теперь нужно  представить в виде суммы полиномов Чебышева:

.

Известно, что   ,          .       найдем по рекуррентной формуле:

;

Выражаем      через полиномы Чебышева:

,           ,              .

Запишем  в общем виде:

.

Для нашего случая: .

Число M можно найти двумя способами. В общем случае:

 или .

В нашем случае:

Ответ: ,    M = 6.