Задание. Отделить решение системы нелинейных уравнений (СНУ) и построить алгоритмы для уточнения решения методом итераций и методом Ньютона с точностью до 0.001.
![]()
Решение
Отделение решения
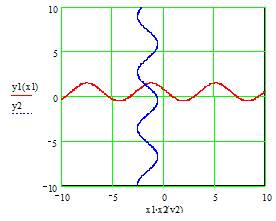
Строим графики и ищем точку пересечения. Область D:{-2 £ x £ -1,5 ; 1.2 £ y £ 2} – выпуклая область (квадрат), которая содержит одно решение СНУ.
Уточнение решения
Алгоритм метода Ньютона
1. Проверим условия на применение метода Ньютона:
![]()
Функции f1 и f2 дважды непрерывно дифференцируемы в области D, определитель матрицы Якоби не равен нулю в области D.
Матрица Якоби имеет вид:
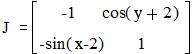 ,
,
![]() , так как
, так как ![]() | для –2 £ x £ -1.5.
| для –2 £ x £ -1.5.
2. Формула метода: ![]() , вектор
, вектор ![]() .
.
3. Выбор начального приближения: х(0)={-2, 1.2}.
4. Условие остановки итерационного процесса: ![]() .
.
Алгоритм метода итераций
1. Условия на применение метода итераций:
![]()
Функции f1 и f2 непрерывно дифференцируемы в области D.
Строим x = Ф(x): 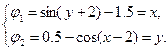
Частные производные имеют вид:
![]() = 0,
= 0, ![]() = cos(y+2),
= cos(y+2), ![]() = sin(x-2),
= sin(x-2), ![]() .
.
Тогда матрица М имеет вид:
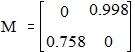 ,
,
|| M || = 0.998 < 1.
2. Формула метода: ![]() , вектор
, вектор ![]() .
.
3 Выбор начального приближения: х0 = {-2, 1.2}.
3. Условие остановки: ![]() (1-||M||)/||M||.
(1-||M||)/||M||.