В экономических исследованиях часто изучаются связи между случайными и неслучайными величинами. Взаимосвязь между исследуемыми факторами и результативным показателем проявится, если взять для исследования большое количество наблюдений (объектов) и сравнить их значения. Тогда в соответствии с законом больших чисел влияние других факторов на результативный показатель сглаживается, нейтрализуется. Это дает возможность установить связь, соотношения между изучаемыми явлениями. Такие связи называют регрессионными, а метод их изучения — регрессионным анализом.
Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений.
Математически задача формулируется следующим образом. Требуется найти аналитическое выражение зависимости экономического явления (например, производительности труда) от определяющих его факторов, т.е. следует определить функцию Y = f(X1, Хг, …, Хп), отражающая в среднем зависимость, по которой, зная значения независимых факторов Хi можно найти приближенное значение зависимого от них показателя Y. В качестве функции в регрессионном анализе принимается случайная переменная, а аргументами являются неслучайные переменные.
Понятие «регрессия» связано с понятием «корреляция». Слово «корреляция» латинского происхождения и в переводе означает «соответствие», «взаимосвязь». Корреляция в широком смысле означает связь, соотношение между объективно существующими объектами, явлениями и процессами. На основе показателей корреляции можно оценить силу или тесноту связи. В корреляционном анализе оценивается сила связи, в регрессионном анализе исследуется ее форма.
На рисунке 3.12 приведена классификация видов регрессии.
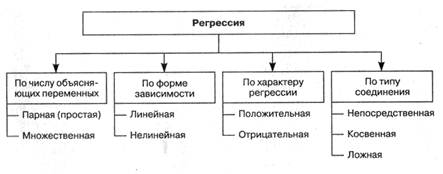
Рис. 3.12 Классификация видов регрессий
Парная (простая) регрессия — регрессия между двумя переменными: результативной и объясняющей (результативным и факторным признаками). Множественная регрессия — регрессия между зависимой переменной и двумя (и более) объясняющими переменными.
Линейная регрессия выражается линейной функцией. Нелинейная регрессия выражается нелинейными функциями.
Положительная регрессия — с увеличением (уменьшением) объясняющей переменной значение зависимой переменной также соответственно увеличивается (уменьшается). Отрицательная регрессия — с увеличением или уменьшением объясняющей переменной зависимая переменная уменьшается или увеличивается.
Непосредственная регрессия — зависимая и объясняющая переменные связаны непосредственно друг с другом. Косвенная регрессия — объясняющая переменная действует на зависимую через ряд других переменных. Ложная регрессия возникает при формальном подходе к исследуемым явлениям без объяснения того, какие причины обусловливают данную связь.
Для нахождения уравнения регрессии необходимо определить общий вид функциональной зависимости и рассчитать параметры уравнения.
Практика регрессионного анализа говорит о том, что уравнение линейной регрессии часто достаточно хорошо выражает зависимость между показателями даже тогда, когда на самом деле они оказываются более сложными. Это объясняется тем, что в пределах исследуемых величин самые сложные зависимости могут носить приближенно линейный характер. В общей форме прямолинейное уравнение регрессии имеет вид:
![]()
где у — результативный признак, исследуемая переменная; xi, — обозначение фактора (независимая переменная); т — общее число факторов; a0 — постоянный (свободный) член уравнения; bi — коэффициент регрессии при факторе.
Значения коэффициентов a и b находят расчетным путем способом наименьших квадратов или с помощью пакета прикладных программ в EXCEL.
Параметр b показывает среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения.
Частным случаем регрессионной функции является тренд (зависимость у от времени t). Поэтому рассмотренные приемы экстраполяции вполне применимы к трендовым регрессиям.
Использование регрессионных моделей в моделировании социально-экономических объектов и процессов осуществляется по многим направлениям в зависимости от вида применяемых функций.