Метод вероятностно-статистической оценки точности основан на проведении обработки опытной партии заготовок с замерами интересующего размера шкальным инструментом (микрометром или другим в зависимости от требуемой точности измерений). Результаты замеров математически обрабатывают, после чего строят кривую распределения исследуемого размера. Для этого в полученном ряде размеров выявляют предельные значения. Разность между наибольшим и наименьшим действительными размерами заготовок в данной партии (Dр) называют размахом распределения, или полем рассеяния размеров:
Dр = lmax – lmin. (3.9)
Полученное значение Dр разбивают на равные интервалы и определяют частость повторения отклонений размеров в каждом интервале:
W = m / n, (3.10)
где m – число заготовок, фактический размер которых находится в пределах данного интервала; n – общее число деталей в партии.
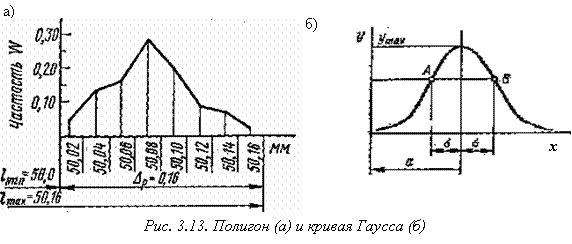
Далее строят график (полигон) распределения размеров. По оси абсцисс откладывают фактические размеры заготовок (или интервалы размеров), а по оси ординат – частость их повторения (w). Например, на графике (см. рис. 3.13, а) общее число деталей в исследуемой партии составляет 100 шт. Поле рассеяния размеров Dp = 0,16 мм. Для построения полигона размеров принято восемь размерных групп с интервалом в 0,02 мм. В первой размерной группе оказалось 5 деталей, т.е. частость w1 = 0,05, во второй группе – 13, т.е. частость w2 = 0,13, и т.д. Полученные точки соединяют прямыми.
Если увеличить число размерных групп (например, принять интервал в 0,01 мм) и увеличить общее число обрабатываемых деталей, то ломаная линия становится более плавной.
Экспериментально установлено, что при обработке заготовок на металлорежущих станках способом автоматического получения размеров точность обработки подчиняется в большей или меньшей степени закону нормального распределения, который изображается математической кривой Гаусса (рис. 3.13, б). Уравнение кривой Гаусса имеет вид:
![]() , (3.11)
, (3.11)
где s – среднее квадратичное отклонение аргумента; е – основание натуральных логарифмов; параметр a является центром группирования значения аргумента и в то же время его средней арифметической.
Среднее квадратичное отклонение (s) определяют по результатам измерений партии заготовок по формуле:
![]() . (3.12)
. (3.12)
Здесь n – число произведенных измерений; xi – значение текущего измерения; хср – среднее арифметическое данных измерений, которое определяется по формуле:
![]() . (3.13)
. (3.13)
Число измерений (n) следует брать 50 или более. При меньшем числе измерений погрешность определения (σ) превышает ± 10 %.
Кривая нормального распределения симметрична. Ордината вершины кривой ymах (рис. 3.13, б) будет при х = а; она определяется из выражения
![]() .
.
Кривая Гаусса имеет точки перегиба на расстояниях х = ± s. Их ординаты равны:
![]()
Величина s характеризует форму кривой распределения и является мерой точности данного метода обработки:
· при увеличении s вершина кривой снижается, но ветви кривой растягиваются, т.е. поле рассеяния размеров растет;
· при уменьшении s ордината кривой возрастает, а поле рассеяния сужается.
На рис.3.14, а схематически показаны кривые распределения последовательно после предварительного точения (кривая s), чистового точения (кривая s1) и шлифования (кривая s2), причем при правильном построении этапов процессов необходимо выполнение условия s > s1 > s2.
Если обрабатываются две партии одноименных заготовок, то появляется систематическая постоянная погрешность, связанная с погрешностью настройки станка на размер или с различными отклонениями размеров режущего инструмента. В этом случае кривые распределения погрешностей при обработке первой и второй партий будут смещены одна относительно другой на размер постоянной погрешности Dн (рис.3.14 б).
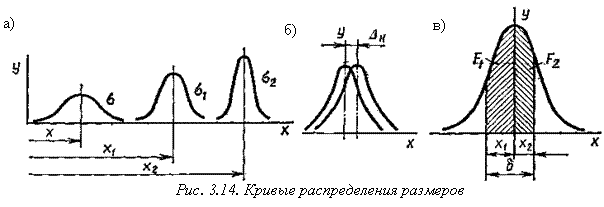
Изучение кривых распределения погрешностей позволяет выявить соотношение между числом годных и бракованных деталей. Предположим, что на обработку заготовок установлен допуск d. На оси абсцисс (рис.3.14, в) этот допуск определяется величинами х1 и х2 от границ центра, диаметральных размеров при обработке партии заготовок группирования. Заштрихованный участок соответствует числу заготовок, находящихся в пределах поля допуска. Отношение площади этого участка к общей площади, ограниченной кривой, определяет вероятность получения годных заготовок, так как площадь, ограниченная кривой нормального распределения, соответствует общему числу заготовок в партии.
Площади F1 и F2 рассчитывают по формулам:
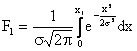 ; (3.14)
; (3.14)
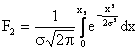 . (3.15)
. (3.15)
Если принять х /s = z, то эти интегралы можно представить в виде функции Ф(z):
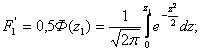 (3.16)
(3.16)
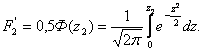 (3.17)
(3.17)
Вся площадь, ограниченная кривой, равна 1. Значения величин ![]() и
и ![]() меньше единицы. Значения функции Ф(z) через десятую долю аргумента приведены в табл. 3.1.
меньше единицы. Значения функции Ф(z) через десятую долю аргумента приведены в табл. 3.1.
Из табл. 3.1 видно, что в интервале z = ± 3, т.е. при х = ± 3s, площадь, ограниченная этим участком кривой, составляет 0,9973 всей площади. Это означает, что 99,73 % всех обработанных заготовок, находящихся в интервале 6s, будут годными, и процент брака не превысит 0,27 %.
Таким образом, определив для исследуемого процесса значение s, можно установить точность данного метода обработки по величине 6s (правило «шести сигм»). Если принять для расчета, например, величину 5s, то процент брака возрастет до 1,24, так как согласно табл. 3.1 Ф(z) будет 0,9876. Возрастание вероятности брака почти в 4,5 раза недопустимо. Правило «шести сигм» является достаточно точным для практических расчетов.
Таблица 3.1
Значения функции Ф(z) через десятую долю аргумента
|
z |
Ф(z) |
z |
Ф(z) |
z |
Ф(z) |
|
0 |
0 |
1,2 |
0,7699 |
2,4 |
0,9836 |
|
0,1 |
0,0797 |
1,3 |
0,8064 |
2,5 |
0,9876 |
|
0,2 |
0,1585 |
1,4 |
0,8385 |
2,6 |
0,9907 |
|
0,3 |
0,2358 |
1,5 |
0,8664 |
2,7 |
0,9931 |
|
0,4 |
0,3108 |
1,6 |
0,8904 |
2,8 |
0,9949 |
|
0,5 |
0,3829 |
1,7 |
0,9109 |
2,9 |
0,9963 |
|
0,6 |
0,4515 |
1,8 |
0,9281 |
3,0 |
0,9973 |
|
0,7 |
0,5161 |
1,9 |
0,9426 |
3,1 |
0,99806 |
|
0,8 |
0,5763 |
2,0 |
0,9545 |
3,2 |
0,99862 |
|
0,9 |
0,6319 |
2,1 |
0,9643 |
3,3 |
0,99903 |
|
1,0 |
0,6827 |
2,2 |
0,9722 |
3,4 |
0,99933 |
|
1,1 |
0,7287 |
2,3 |
0,9786 |
3,5 |
0,99953 |