Текущее управление качеством связано с контролем технологических процессов. Определяются контрольные параметры технологического процесса. Выход за пределы допустимого диапазона контрольных параметров может привести к выпуску бракованной продукции. Отклонения параметров происходят под воздействием случайных факторов. Для контроля качества технологических процессов применяются статистические методы. Наиболее распространены следующие методы.

1) Диаграмма Парето, которая используется для оценки частоты появления брака (отклонения в размерах деталей, некачественное сырье, нарушение технологи-ческого процесса и др.).

Опыт исследования частоты брака показывает, что малое число видов брака составляет большую долю общего числа. Суммарная частота появления брака категории "прочие" не должна превышать  10 %, т. е. в прочие должны входить виды брака, суммарная доля которых не превышает 10 %.

2) Схема Исикавы – "рыбий скелет", которая отражает логическую структуру отношений между элементами, этапами, работами, составляющими изучаемый технологический процесс. Схема строится по принципу четырех компонентов, влияющих на качество продукции: материал, машины, сырье, люди. При ее построении факторы располагаются по значимости (ближе к цели строится более значимый фактор). При этом каждый фактор проходит свой цикл предварительной обработки и может быть разбит на более мелкие,  более детализированные схемы (см. схему).

Операции, составляющие обработку, показаны стрелками. Каждая стрелка сопряжена с оценками тех или иных показателей. Например, изделие нагревается, возникает необходимость в контроле температурного режима. "Рыбий скелет является инструментом логического решения задачи.

Схема может применяться при анализе качества изделий в целом, а также отдельных этапов его изготовления.

3) Одним из основных инструментов в обширном арсенале статистических методов контроля качества являются контрольные карты. Принято считать, что идея контрольной карты принадлежит известному американскому статистику Уолтеру Л. Шухарту. Она была высказана им в 1924 г. и обстоятельно описана в 1931 г. Первоначально они использовались для регистрации результатов измерений требуемых

свойств продукции. Выход параметра за границы поля допуска свидетельствовал о необходимости остановки производства и проведении корректировки процесса в соответствии со знаниями специалиста, управляющего производством.

Это давало информацию о том, когда, кто, на каком оборудовании получал брак в прошлом.

Однако в этом случае решение о корректировке принималось тогда, когда брак уже был получен. Поэтому важно было найти процедуру, которая бы накапливала информацию не только для ретроспективного исследования, но и для использования при принятии решений. Это предложение опубликовал американский статистик И. Пейдж в 1954 г. Карты, которые используются при принятии решений, называются кумулятивными.

Контрольная карта (рис. 6.2) состоит из центральной линии, двух контрольных пределов (над и под центральной линией) и значений характеристики (показателя качества), нанесенных на карту для представления состояния процесса.

В определенные периоды времени отбирают (все подряд; выборочно; периодически из непрерывного потока и т. д.) n изготовленных изделий и измеряют контролируемый параметр.

Результаты измерений наносят на контрольную карту и, в зависимости от этого значения, принимают решение о корректировке процесса или о продолжении процесса без корректировок.

Сигналом о возможной разналадке технологического процесса могут служить:

- выход точки за контрольные пределы (точка 6); (процесс вышел из-под конт-роля);

- расположение группы последовательных точек около одной контрольной границы, но не выход за нее (11, 12, 13, 14), что свидетельствует о нарушении уровня настройки оборудования;

- сильное рассеяние точек (15, 16, 17, 18, 19, 20) на контрольной карте относительно средней линии, что свидетельствует о снижении точности технологического процесса.

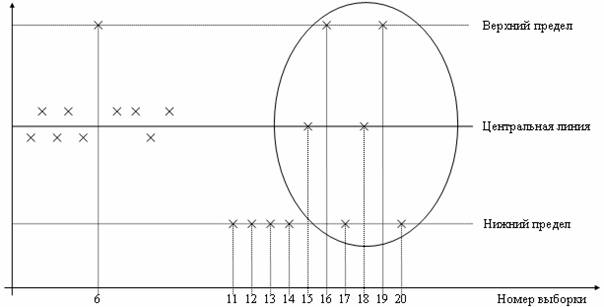
Рис. 6.2 Контрольная карта

При наличии сигнала о нарушении производственного процесса должна быть выявлена и устранена причина нарушения.

Таким образом, контрольные карты используются для выявления определенной причины, но не случайной.

Под определенной причиной следует понимать существование факторов, которые допускают изучение. Разумеется, что таких факторов следует избегать.

Вариация же, обусловленная случайными причинами, необходима, она неизбежно встречается в любом процессе, даже если технологическая операция проводится с использованием стандартных методов и сырья. Исключение случайных причин вариации невозможно технически или экономически нецелесообразно.

Часто при определении факторов, влияющих на какой-либо результативный показатель, характеризующий качество, используют схемы Исикава.

Они были предложены профессором Токийского университета Каору Исикава в 1953 г. при анализе различных мнений инженеров. Иначе схему Исикава называют диаграммой причин и результатов, диаграммой "рыбий скелет", деревом и т. д.

Она состоит из показателя качества, характеризующего результат и факторных показателей (рис. 6.3).

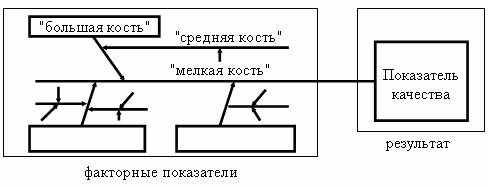
Рис. 6.3 Структура диаграммы причин и результатов

Построение диаграмм включает следующие этапы:

1) Выбор результативного показателя, характеризующего качество изделия (процесса и т. д.).

2) Выбор главных причин, влияющих на показатель качества. Их необходимо поместить в прямоугольники ("большие кости").

3) Выбор вторичных причин ("средние кости"), влияющих на главные.

4) Выбор (описание) причин третичного порядка ("мелкие кости"), которые влияют на вторичные.

5) Ранжирование факторов по их значимости и выделение наиболее важных.

Диаграммы причин и результатов имеют универсальное применение. Так, они широко применяются при выделении наиболее значимых факторов, влияющих, например, на производительность труда.

Отмечается, что число существенных дефектов незначительно и вызываются они, как правило, небольшим количеством причин. Таким образом, выяснив причины появления немногочисленных существенно важных дефектов, можно устранить почти все потери.

Эта проблема может решаться с помощью диаграмм Парето.

Различают два вида диаграмм Парето:

1) по результатам деятельности. Они служат для выявления главной проблемы и отражают нежелательные результаты деятельности (дефекты, отказы и т. д.);

2) по причинам (факторам). Они отражают причины проблем, которые возникают в ходе производства.

Рекомендуется строить много диаграмм Парето, используя различные способы классификации как результатов, так и причин, приводящих к этим результатам.

Лучшей следует считать такую диаграмму, которая выявляет немногочисленные, существенно важные факторы, что и является целью анализа Парето.

Построение диаграмм Парето включает следующие этапы:

1) Выбор вида диаграммы (по результатам деятельности или по факторам).

2) Классификация результатов (причин). Разумеется, что любая классификация имеет элемент условности, однако, большинство наблюдаемых единиц какой-либо совокупности не должны попадать в строку "прочие".

3) Определение метода и периода сбора данных.

4) Разработка контрольного листка для регистрации данных с перечислением видов собираемой информации. В нем необходимо предусмотреть свободное место для графической регистрации данных.

5) Ранжирование данных, полученных по каждому проверяемому признаку в порядке значимости. Группу "прочие" следует приводить в последней строке вне зависимости от того, насколько большим получилось число.

6) Построение столбиковой диаграммы (рис. 6.4).

Значительный интерес представляет построение диаграмм Парето в сочетании с диаграммой причин и следствий.

Выявление главных факторов, влияющих на качество продукции, позволяет увязать показатели производственного качества с каким-либо показателем, характеризующим потребительское качество.

Для такой увязки возможно применение регрессионного анализа.

Например, в результате специально организованных наблюдений за результатами носки обуви и последующей статистической обработки полученных данных было установлено, что срок службы обуви (у), зависит от двух переменных: плотности материала подошвы в г/см³ (х1) и предела прочности сцепления подошвы с верхом обуви в кг/см² (х2). Вариация этих факторов на 84,6 % объясняет вариацию результативного признака (множественный коэффициент коррекции R=0,92), а уравнение регрессии имеет вид:

у = 6,0 + 4,0 * х1 + 12 * х2.

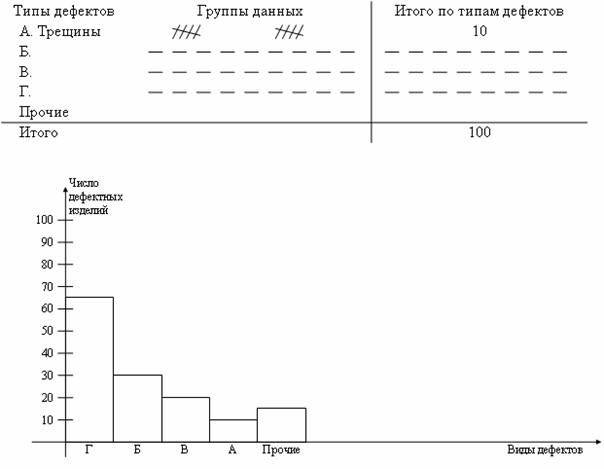
Рис. 6.4 Связь между видами дефектов и числом дефектных изделий

Таким образом, уже в процессе производства, зная характеристики факторов х1 и х2, можно прогнозировать срок службы обуви. Улучшая вышеназванные параметры, можно увеличить срок носки обуви. Исходя из необходимого срока службы обуви, можно выбирать технологически допустимые и экономически оптимальные уровни признаков производственного качества.

Наибольшее практическое распространение имеет характеристика качества изучаемого процесса путем оценки качества результата этого процесса. В этом случае речь идет о контроле качества изделий, деталей, получаемых на той или иной операции. Наибольшее распространение имеют несплошные методы контроля, а наиболее эффективны те из них, которые базируются на теории выборочного метода наблюдения.

Пример 6.2.На электроламповом заводе цех производит электрические лампы.

Для проверки качеств ламп отбирают совокупность 25 штук и подвергают испытанию на специальном стенде (меняется напряжение, стенд подвергается

вибрации и т. д.). Каждый час снимают показания о продолжительности горения ламп. Получены следующие результаты:

6; 6; 4; 5; 7;

5; 6; 6; 7; 8;

5; 7; 7; 6; 4;

5; 6; 8; 7; 5;

7; 6; 5; 6; 6.

Прежде всего необходимо построить ряд распределения.

Продолжительность горения (х)	Частота (f)	x*f			В % к итогу	Накопленный процент
4	2	8	4	8	8	8
5	6	30	6	6	24	32
6	9	54	0	0	36	68
7	6	42	6	6	24	92
8	2	16	4	8	8	100
	25	150	20	28	100	–

Затем следует определить:

1) среднюю продолжительность горения ламп:

 ч;

2) моду (вариант, который чаще всего встречается в статистическом ряду). Она равна 6;

3) медиану (значение, которое расположено в середине ряда). Это такое значение ряда, которое делит его численность на две равные части. Медиана равна также 6.

Построим кривую распределения (полигон) (рис. 6.5).

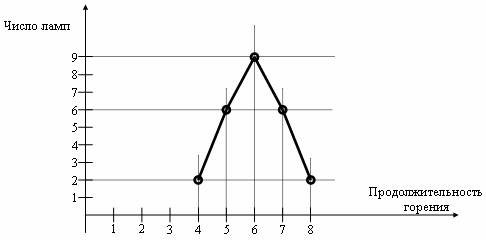
Рис. 6.5 Распределение ламп по продолжительности горения

Определим размах:

R=Х_max–Х_min=4ч.

Он характеризует пределы изменения варьирующего признака. Среднее абсолютное отклонение:

Это средняя мера отклонения каждого значения признака.

Среднее квадратическое отклонение:

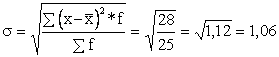ч.

Рассчитаем коэффициенты вариации:

1) по размаху:

;

2) по среднему абсолютному отклонению:

;

3) по среднему квадратическому отношению:

.

С точки зрения качества продукции, коэффициенты вариации должны быть      минимальными.

Так как завод интересует не качество контрольных ламп, а всех ламп, возникает вопрос о расчете средней ошибки выборки:

ч.

которая зависит от колеблемости признака и от числа отобранных единиц (n).

Доверительное число t показывает, что расхождение не превышает кратную ему ошибку выборки. С вероятностью 0,954 можно утверждать, что разность между выборочной и генеральной не превысит двух величин средней ошибки выборки, то есть в 954 случаях ошибка репрезентативности не выйдет за 2:

;

.

Таким образом, с вероятностью 0,954 ожидается, что средняя продолжительность горения будет не меньше, чем 5,6 ч и не больше, чем 6,4 ч. С точки зрения качества продукции, необходимо стремиться к уменьшению этих отклонений.

Обычно при статистическом контроле качества допустимый уровень качества, который определяется количеством изделий, прошедших контроль и имевших качество ниже минимально приемлемого, колеблется от 0,5 % до 1 % изделий. Однако для компаний, которые стремятся выпускать продукцию только высшего качества, этот уровень может быть недостаточным. Например, "Toyota" стремится свести уровень брака к нулю, имея в виду, что хотя и выпускаются миллионы автомобилей, но каждый покупатель приобретает лишь один из них. Поэтому, наряду со статистическими

методами контроля качества, на фирме разработаны простые средства контроля качества всех изготавливаемых деталей (TQM). Статистический контроль качества в первую очередь применяется в отделениях фирмы, где продукция изготавливается партиями. Например, в лоток высокоскоростного автоматического процесса после обработки поступает 50 или 100 деталей, из которых контроль проходят только первая и последняя. Если обе детали не имеют дефектов, то все детали считаются хорошими. Однако, если последняя деталь окажется бракованной, то будет найдена и первая дефектная деталь в партии, а весь брак будет изъят. Для того чтобы ни одна партия не избежала контроля, пресс автоматически отключается после обработки очередной партии заготовок. Применение выборочного статистического контроля имеет эффект всеобъемлющего тогда, когда каждая производственная операция выполняется стабильно, благодаря тщательной отладке оборудования, использованию качественного сырья и т. д.

Большую роль в обеспечении качества играет статистический приемочный контроль.