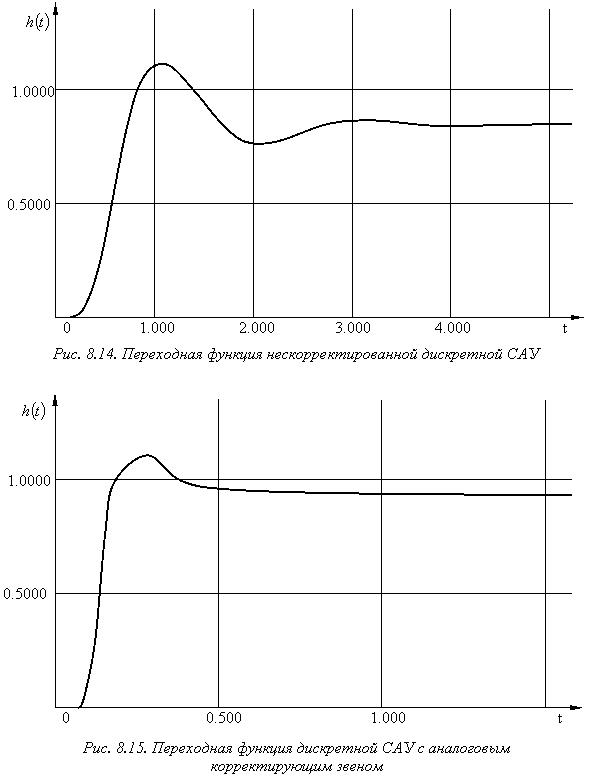
Конечная цель расчетно-графического задания состоит в синтезе САР, удовлетворяющей ряду требований к показателям качества регулирования системы. Цель считается достигнутой, если определены структура и параметры корректирующего устройства, обеспечивающего достаточно хорошее приближение характеристик системы к желаемым.
Кроме указанных в задании требований к статической точности, времени регулирования и перерегулирования, при синтезе корректирующих устройств дискретных САР можно задаваться и другими критериями, например желаемым характером реакции системы на определенное входное воздействие или условием конечной длительности переходного процесса.
В отличие от непрерывных САР в дискретных системах применяют два способа коррекции – непрерывный и дискретный. При первом способе коррекция осуществляется введением в систему непрерывных (аналоговых) корректирующих устройств, при втором способе – введением импульсных фильтров или цифровых регуляторов.
Реализуем указанные способы применительно к системе, параметры которой приведены в последней строке таблицы вариантов численных значений параметров звеньев нескорректированной САУ. Для достижения приемлемой точности результатов при всех вычислениях необходимо учитывать не менее трех значащих цифр.
1. Передаточная функция разомкнутой нескорректированной системы при наличии в ней фиксатора в качестве формирующего элемента определяется следующим образом:
,
где 
– передаточные функции непрерывной части разомкнутой системы и фиксатора соответственно.
Для рассматриваемой САР:
.
Передаточная и модифицированная передаточная функции замкнутой нескорректированной системы вычисляются по формулам:
и 
,
где 
- передаточная и модифицированная передаточная функции прямой цепи САР. Для систем с единичной обратной связью 
и 
совпадают.
Для рассматриваемой системы:
;
,
где
;
;
.
Передаточная функция 
может быть получена из выражения для 
:
.
Зная выражения для и , можно записать 
-изображения реакции системы на единичное ступенчатое воздействие:
.
1. Корни характеристического уравнения замкнутой нескорректированной системы, рассматриваемой в качестве примера, равны:
.
Модуль корней 
, т.е. корни лежат внутри единичной окружности с центром в начале координат комплексной плоскости . Следовательно, система устойчива.
Аналогичный вывод может быть сделан, если для оценки устойчивости использовать билинейное преобразование. После подстановки 
характеристическое уравнение замкнутой системы примет вид:
При использовании указанного преобразования условия устойчивости непрерывных и дискретных систем совпадают, вследствие чего совпадают и методы оценки устойчивости. Так, согласно критерию Рауса-Гурвица необходимым и достаточным условием устойчивости САУ второго порядка является положительность коэффициентов характеристического уравнения. Это условие для рассматриваемой системы выполняется.
2. Начальное и установившееся значения решетчатой функции 
определяются по -изображению 
на основании соответствующих теорем -преобразования:
; (8.1)
, (8.2)
причем выражение (8.2) справедливо при условии, что выражение 
не имеет полюсов за пределами окружности единичного радиуса и на самой окружности с центром в начале координат комплексной плоскости .
Если выходной сигнал системы представляет собой реакцию на единичное ступенчатое воздействие, то выражения (8.1) – (8.2) могут быть преобразованы к виду:
; 
.
Для определения искомых значений решетчатой функции можно воспользоваться и модифицированным -изображением 
. В этом случае соответствующие выражения имеют вид:
;
.
Для рассматриваемой системы:
;
.
Из последнего выражения следует, что установившаяся ошибка системы равна 0,163.
1. Для большинства реальных дискретных САУ порядок числителя 
передаточной функции замкнутой системы ниже порядка ее знаменателя 
. Для них при определении выражения для решетчатой функции, описывающей реакцию системы на единичное ступенчатое воздействие, можно воспользоваться формулой:
, (8.3)
где 
– порядок характеристического уравнения замкнутой системы; 
– корень характеристического уравнения; 
.
Для рассматриваемой САУ дискретные значения выходного сигнала системы, наблюдаемые в моменты квантования, вычисляются по формуле:
.
Значения решетчатой функции 
, вычисленные при 
и 
, должны совпадать соответственно с начальным и установившимся значениями выходного сигнала системы, определенными по формулам (8.1) и (8.2).
Для нахождения 
модифицированное 
-изображение выходного сигнала представляется в виде суммы трех слагаемых:
.
Каждому из них соответствует одно из трех слагаемых в выражении решетчатой функции . Для определения первых двух может быть использована формула (8.3). При этом, вычисляя первое слагаемое модифицированной решетчатой функции, следует считать равным 
, а при вычислении второго слагаемого 
.
Третье слагаемое 
не имеет нулевого корня, поэтому при вычислении третьей составляющей полагаем 
, но параметр 
в формуле
(8.3) заменяем на 
. При вычислении всех трех слагаемых в выражении 
считаем, что
.
Для произвольных моментов времени 
значение выходного сигнала рассматриваемой системы равно:
.
Здесь 
.
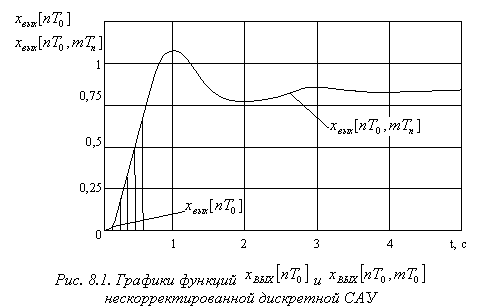
На рис. 8.1 приведены графики функций 
и .
1. 
Построение логарифмических амплитудно- и фазочастотных характеристик (ЛАХ и ФЧХ) дискретных систем выполняется в функции абсолютной псевдочастоты 
, связанной с частотой 
следующей зависимостью:
.
Переход к частотным характеристикам производится в два этапа.
Первоначально необходимо вычислить передаточную функцию 
, для чего в передаточной функции нескорректированной системы 
переменная 
полагается равной:
.
Затем в полученном выражении делается замена 
.
Построение асимптотической ЛАХ 
по виду 
производится по тем же правилам, что и для непрерывных систем. При построении ФЧХ 
следует об
ращать внимание на наличие неминимально-фазового сомножителя 
в числители функции 
. Определяемая им составляющая 
равна:
.
Для рассматриваемой системы:
;
.
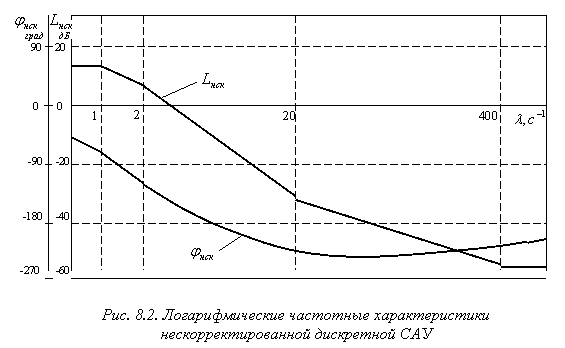
Логарифмическая амплитудно-частотная характеристика и ФЧХ нескорректированной разомкнутой системы приведены на рис. 8.2.
1. Один из возможных способов коррекции дискретных САУ основывается на использовании аналогового корректирующего звена, включенного последовательно в непрерывную часть системы, как показано на рис. 8.3. При этом передаточная функция разомкнутой скорректированной системы равна:
. (8.4)
 |
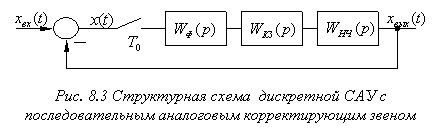Для нахождения передаточной функции 
необходимо предварительно определить желаемую передаточную функцию 
. С этой целью сначала строится желаемая ЛАХ разомкнутой скорректированной системы 
. Построение осуществляется по методикам, разработанным для непрерывных САУ, с учетом всех требований, предъявляемых к дискретной системе.
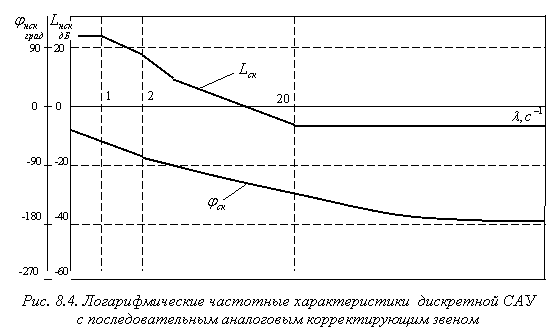
Для рассматриваемого примера вид желаемых характеристик и 
приведен на рис. 8.4. Частотная характеристика дискретной САУ с фиксатором обязательно имеет в числителе сомножитель , поэтому выбранной желаемой ЛАХ соответствуют следующие выражения для 
и :
,
.
Запас по фазе в скорректированной системе составляет 
.
От осуществляется переход к передаточной функции 
, для чего используется подстановка 
. Далее, полагая 
, преобразуем передаточную функцию к выражению для 
.
Для рассматриваемой системы:
;
.
Если передаточная функция 
определена, то на основании выражения (8.4) можно найти выражение 
, являющееся 
-изображением функции 
:
.
 |
Затем следует определить 
, для чего необходимо выполнить операцию обратного -преобразования:
. (8.5)
Проще всего такое преобразование выполняется, если функция включена в таблицу -преобразований. В противном случае можно разложить на простые слагаемые, для каждого из которых функция-оригинал находится по таблице.
Другой путь выполнения обратного -преобразования заключается в следующем:
· по определяется решетчатая функция 
, которая с помощью подстановки 
преобразуется в непрерывную функцию 
;
· затем осуществляется преобразование Лапласа функции , в результате чего определяется искомое выражение .
Передаточная функция последовательного аналогового корректирующего звена равна:
. (8.6)
Полученная передаточная функция 
должна быть физически реализуемой. Для этого количество полюсов должно быть не меньше числа нулей. Полюса функции должны находиться в левой половине 
-плоскости. Если необходи
мо, чтобы корректирующее звено реализовывалось с помощью 
-схем, передаточная функция 
не должна иметь кратных полюсов.
Для рассматриваемой системы:
.
По таблице 
-преобразований находим:
.
Согласно (8.6) передаточная функция корректирующего звена равна:
. (8.7)
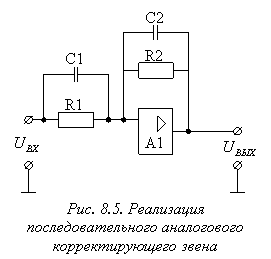Для обеспечения физической реализуемости необходимо ввести в передаточную функцию (8.7) дополнительный достаточно удаленный полюс, существенно не снижающий эффективности коррекции.
Окончательно полагаем:
.
(8.8)
Корректирующее звено с такой передаточной функцией может быть реализовано на одном операционном усилителе по схеме, приведенной на рис. 8.5. Расчет элементов схемы осуществляется исходя из следующих соотношений:
.
Рассмотренный способ последовательного включения корректирующего звена не является единственно возможным. На рис. 60 приведена структурная схема дискретной САУ, коррекция которой осуществляется аналоговым регулятором, включенным в цепь обратной связи.
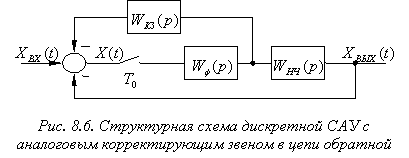В этом случае передаточные функции разомкнутой скорректированной системы и корректирующего звена равны:
;
,
где выражение 
определено по формуле (8.5).
Возможны и такие дискретные САУ, для коррекции которых аналоговые регуляторы включаются как в прямую цепь, так и в цепь обратной связи.
1. На рис. 8.7 приведена структурная схема системы, коррекция которой осуществляется последовательным дискретным регулятором.
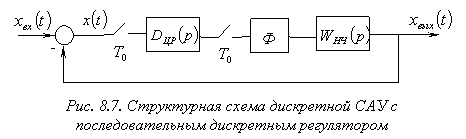Передаточная функция разомкнутой скорректированной системы равна:
.
Логарифмические амплитудно- и фазочастотные характеристики такой системы:
.
Если на основании требований к качеству регулирования определен вид 
, можно построить ЛАХ корректирующего звена:
. (8.9)
Дальнейшая последовательность действий аналогична рассмотренной в предыдущем пункте 6:
· по виду 
определяем выражение 
;
· далее, полагая 
, производим переход к 
;
· затем, используя подстановку 
, можно записать передаточную функцию 
.
Полученная передаточная функция должна быть физически реализуемой. Для этого порядок знаменателя должен быть больше порядка числителя или равен ему.
При построении для данного способа коррекции, учитывая все требования к качеству регулирования, необходимо также стремиться получить достаточно простой вид ЛАХ корректирующего звена. Это обеспечит приемлемую сложность при его реализации.
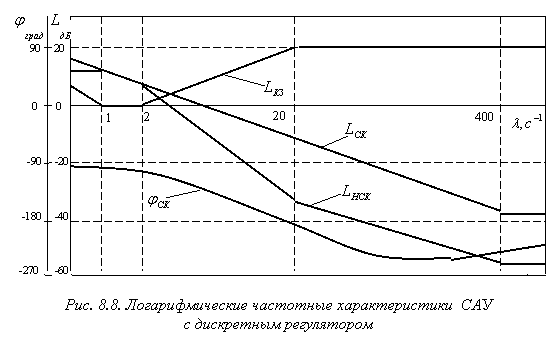
Синтез дискетного корректирующего звена для рассматриваемой САУ осуществляется с учетом более жестких требований к точности по сравнению с рассмотренным вариантом непрерывной коррекции. Необходимо обеспечить нулевое значение установившейся ошибки по положению и добротность по скорости не менее пяти. С учетом этих, а также остальных требований к качеству регулирования, перечисленных в задании, построены логарифмические амплитудно-частотные характеристики скорректированной системы (рис. 8.8).
Амплитудно-фазовая характеристика скорректированной системы полагается равной:
.
На рис. 8.8 приведены также ЛАХ нескорректированной системы и корректирующего звена. Построение последней осуществлялось по формуле (8.9).
Амплитудно-фазовая характеристика корректирующего звена описывается выражением:
.
 |
При этом передаточная функция регулятора, записанная с использованием переменной 
, равна:
.
Искомая передаточная функция регулятора описывается выражением:
. (8.10)
1. Использование цифрового вычислительного устройства в качестве регулятора предполагает разработку соответствующей программы ЦВУ, отчего методы реализации передаточной функции 
называются иногда методами программирования.
Заданной функции могут соответствовать различные программы. Выбор метода программирования определяется объектом памяти ЦВУ, его быстродействием, разрядностью и т.д. К числу основных относятся параллельный, последовательный и прямой методы программирования. Последний из них был использован при реализации дискретного регулятора для рассматриваемой САУ.
Передаточную функцию (8.10) запишем в виде:
, (8.11)
где 
– 
-изображения входного и выходного сигналов регулятора.
Следовательно:
. (8.12)
Выполнив обратное -преобразование над обеими частями последнего выражения, получим:
.
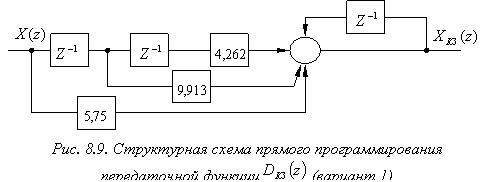
Из выражения (8.12) следует, что очередное дискретное значение выходного регулятора определяется очередным и двумя предшествующими значениями входного
сигнала, а также предшествующим значением выходного сигнала. Алгоритм работы ЦВУ, описываемый рекуррентным выражением (8.12), отражен на структурной схеме, приведенной на рис. 8.9. В ней 
- элемент задержки сигнала на один период квантования. Для реализации такого регулятора требуется три элемента задержки.
При другом варианте прямого метода программирования может быть получен алгоритм работы ЦВУ, отличный от выражения (8.12).
Согласно выражению (8.11):
. (8.13)
Введем фиктивную переменную:
. (8.14)
Тогда:
. (8.15)
Выражение (8.15) преобразуем к виду:
. (8.16)
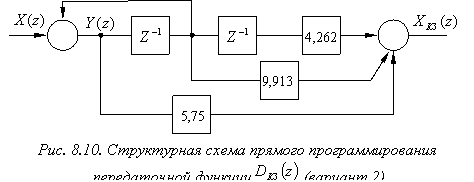На основании выражений (8.15) и (8.16) формируется алгоритм управления ЦВУ, предполагающий использование только двух элементов задержки (рис. 8.10). Соответствующие данному алгоритму рекуррентные зависимости для вычисления текущего значения 
имеют вид:
,
где 
1. Другой способ реализации дискретного корректирующего звена предполагает использование импульсного фильтра.
Импульсный фильтр – это электрический четырехполюсник, включенный между двумя устройствами выборки и хранения дискретных значений сигналов.
На рис. 8.11 приведена структура последовательного ИФ, для которого справедлива следующая зависимость между 
и 
:
, (8.17)
где – передаточная функция четырехполюсника.
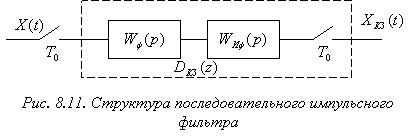Если выражение для определено, искомая передаточная функция находится по методике, совпадающей с той, что была использована при определении последовательного непрерывного корректирующего звена. На основании выражения (8.17) можно записать:
.
Передаточная функция может быть реализована последовательным ИФ на базе 
-четырехполюсника, если:
· порядок знаменателя не меньше порядка числителя;
· значения нулей являются произвольными, а полюса должны быть простыми, положительными и меньшими единицы.
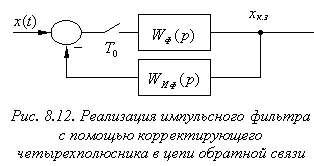При включении четырехполюсника в цепь обратной связи (рис. 8.12) передаточная функция дискретного корректирующего звена определяется следующим выражением:
,
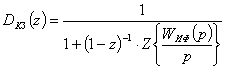преобразуя которое, получаем искомую передаточную функцию четырехполюсника:
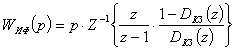. (8.18)
Передаточная функция может быть реализована импульсным фильтром с -четырехполюсником в цепи обратной связи, если:
· имеет одинаковое число полюсов и нулей;
· значения полюсов являются произвольными, а нули должны быть простыми, положительными и меньшими единицы.
Для рассматриваемой системы описывается выражением (8.10). С учетом ограничений, накладываемых на передаточную функцию корректирующего звена, его
реализация возможна в виде ИФ с 
-схемой в цепи обратной связи. Определение 
существенно упрощается, если 
представить в виде:
,
где 
; 
.
При этом корректирующее звено представляет собой последовательно соединенные ИФ и пропорциональное звено с коэффициентом 
.
Тогда в соответствии с выражением (8.18) имеем:
=
.
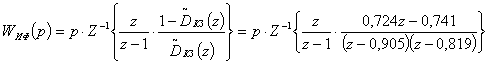Схемное решение, соответствующее полученной передаточной функции , приведено на рис. 8.13 .
1. 
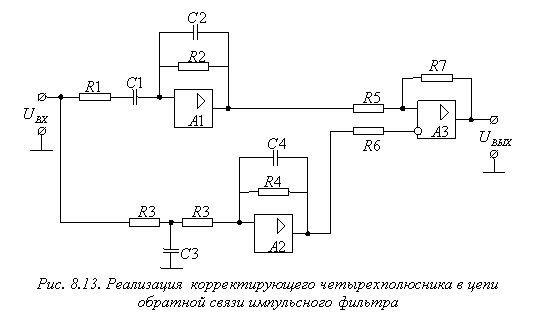Дискретные САУ содержат в своем составе как дискретные, так и непрерывные звенья. Моделирование последних с использованием программы PSM не вызывает затруднений. К числу дискретных звеньев системы относятся импульсные элементы и дискретное корректирующее звено.
Импульсный элемент состоит из последовательно соединенных простейшего импульсного элемента (квантователя) и формирующего элемента. Выходной сигнал первого из них представляет собой последовательность модулированных 
-функций. Поэтому принципиально возможны только упрощенное моделирование квантователя, предполагающее выделение дискрет из его непрерывного входного сигнала, и модуляция ими импульсов большой амплитуды и малой длительности.
Гораздо проще осуществить моделирование ИЭ, содержащего фиксатор в качестве формирующего элемента. Выходной сигнал такого ИЭ изменяется только в моменты квантования, а внутри интервалов квантования остается постоянным, совпадая по зна
чению с очередной дискретой входного сигнала. Существующая версия PSM содержит такое звено – это устройство квантования по времени.
При моделировании САУ, содержащей цифровой регулятор, элементы задержки, входящие в его структуру, моделируются звеньями чистого (транспортного) запаздывания, у которых время запаздывания полагается равным интервалу квантования.
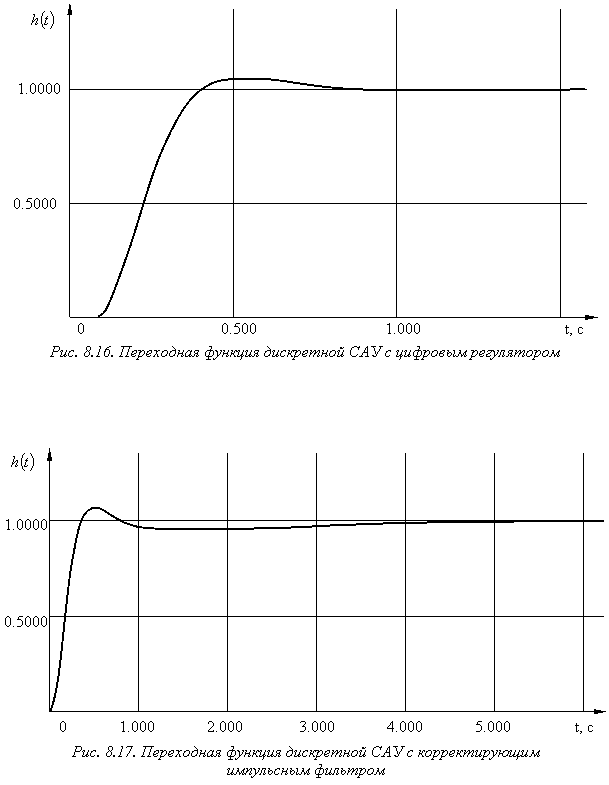
Результаты моделирования приведены на рис. 8.14 – 8.17.
