I.ОБЩИЕ СВЕДЕНИЯ

Производственная программа является ведущим разделом плана предприятия, на основе которого осуществляются расчеты планов по труду и заработной плате, себестоимости, прибыли и рентабельности, материально – технического снабжения. Поэтому выбор оптимального варианта производственной программы является одной из важнейших задач планирования.

Оптимизация производственной программы означает нахождение из множества возможных планов такого варианта, который в заданных условиях производства обеспечивает получение наилучшего результата производственной деятельности при минимальных затратах трудовых, материальных и финансовых ресурсов. Критерием оптимальности программы могут служить либо максимальные прибыли или объем нормативной чистой продукции, либо минимальные совокупные текущие затраты (себестоимость) при производстве заданного объема продукции. В первом случае задача оптимизации решается на максимум, во втором на минимум.

Задача расчета оптимальной программы цеха является экономико – математической задачей, решаемой посредством методов линейного программирования. Экономико – математическая модель состоит из целевой функции и системы ограничений.

ЗАДАНИЕ

Определить оптимальную производственную программу механического цеха, выпускающего на имеющемся оборудовании изделия двух наименований – кронштейн и вал. Технологический процесс изготовления изделий состоит из четырех операций – токарной, фрезерной, сверлильной и шлифовальной. В качестве исходных данных заданы: затраты времени на изготовление одного изделия, пропускная способность оборудования, а также расход ресурсов – материалов, фонда заработной платы, нормативно-чистой продукции. Известна оптовая цена реализации изделий. Указаны лимиты ресурсов на предприятии. Исходные данные, характеризующие технологический процесс изготовления изделий и лимит ресурсов, представлены в табл. 3 и 4.

ИСХОДНЫЕ ДАННЫЕ

Таблица 3

Технологический процесс

Группа  оборудования	Пропускная способность оборудования, ч.	Затраты времени на изготовление одного изделия, ч
		Кронштейн	Вал
Токарная	98705	2	2
Фрезерная	78964	2	1
Сверлильная	59223	1	3
Шлифовальная	47378	1	2

Таблица 4

Ограничения по ресурсам

Ресурсы	Затраты на единицу изделия		Лимит ресурсов на программу
	Кронштейн	Вал
Материалы, кг	3,0	2,0	не более 80000
Основная заработная плата производственных рабочих, р.	1,5	2,0	не более 60000
Норматив чистой продукции, р.	6,0	4,0	max
Оптовая цена изделия, р.	10,0	12,0	-
Планируемый объем реализации, тыс. р.	-	-	не менее 250000

РЕШЕНИЕ

1.   Введем обозначения искомых переменных. Пусть Х1 – искомое количество выпуска кронштейнов (шт.), Х2 – количество валов (шт.).

2. Составим целевую функцию. В нашем примере в качестве целевой функции целесообразно взять максимальный объем выпуска продукции, выраженный показателем «нормативная чистая продукция» (НЧП), так как в исходных данных значком «max» определена цель предприятия – получить как можно больше натурально-чистой продукции.

            Целевая функция примет вид:

Z(X) = НЧПi * Xi  max,

где Z(X) — целевая функция, р.; Xi — количество изделий i – го наименования в оптимальном варианте производственной программы, шт.; НЧПi – норматив чистой продукции единицы i – го изделия, р.

            Подставив в нее исходные данные, получим:

Z(x) = 6x₁ + 4x₂max

3. Составим систему ограничений по ресурсам. В качестве ограничений по ресурсам следует представить: пропускную способность оборудования, количество материала, фонд заработной платы и объем реализации продукции.

            Ограничение по времени работы оборудования (пропускной способности):

Ограничение по пропускной способности оборудования (предусматривает соответствие пропускной способности оборудования трудоемкости производственной программы) можно записать в виде:

tij * Xi  Пj,

где tij – трудоемкость изготовления единицы i – го изделия на j – м оборудовании, ч; Пj, — пропускная способность оборудования j – го вида, ч.

Подставив исходные данные, получим следующие неравенства – ограничения:

2x₁ + 2x₂  98705 – ограничение по времени работы токарного оборудования;

x₁ + 2x₂  78964 — ограничение по времени работы фрезерного оборудования;

3x₁ + x₂  59223 — ограничение по времени работы сверлильного оборудования;

2x₁ + x₂  47378 — ограничение по времени работы шлифовального оборудования.

Ограничение по материалам (отражает соответствие расхода материальных ресурсов по оптимальному плану выделенным предприятию фондам)

Cid * Xi  Md,

где Cid норма расхода материала d – го вида на единицу i – го изделия, кг; Md – количество материальных ресурсов. Неравенство ограничения по материалам примет вид:

3x₁ + 2x₂  80000

Ограничение по фонду заработной платы (лимитирует расходование установленного предприятию фонда заработной платы)

qiXi  Фк,

где  qi – норматив заработной платы основных производственных рабочих на I р. НЧП по i – му изделию; Фк – фонд заработной платы основных производственных рабочих, р.

            При подстановке значений исходных данных ограничение по заработной плате примет вид:

1,5x₁ + 2x₂  60000

Ограничение по объему реализации продукции (гарантирует выполнение предприятием установленному ему задания по объему реализации продукции)

ЦiXi  Vp,

где Цi – отпускная цена реализации единицы i – го изделия, р.; Vp – объем реализации продукции, р. После постановки заданных значений получим:

10x₁ + 12x₂  250000

Обязательным условием данной задачи является неотрицательность полученных значений:

Xi  0,

4. Построим экономико – математическую модель. Экономико математическая модель, состоящая из целевой функции и системы ограничений, имеет следующий вид:

Z(x) = 6x₁ + 4x₂max

1)2x₁ + 2x₂  98705;

2)x₁ + 2x₂  78964;

3)3x₁ + x₂  59223;

4)2x₁ + x₂  47378;

5)3x₁ + 2x₂  80000;

6)1,5x₁ + 2x₂  60000;

7)10x₁ + 12x₂  250000,

где x₁ – объем выпуска кронштейнов, шт. ; x₂  — объем выпуска валов шт.

5. Найдем оптимальную производственную программу предприятия. Нахождение оптимального варианта программы можно осуществить тремя способами: графически, с помощью симплекс – метода и с помощью программы EXCEL «Поиск решения». Здесь рассмотрен графический способ расчета, который удобен при двух переменных. Рассмотрим его на примере приведенной экономико – математической модели.

Графический способ расчета.

• Приравняем левые и правые части всех неравенств из системы ограничений:

1)2x₁ + 2x₂ = 98705;

2)x₁ + 2x₂ = 78964;

3)3x₁ + x₂ = 59223;

4)2x₁ + x₂ = 47378;

5)3x₁ + 2x₂ = 80000;

6)1,5x₁ + 2x₂ = 60000;

                                                            7)10x₁ + 12x₂ = 250000

Каждое ограничение приняло вид: а₁x₁ + a₂x₂ = b, которое графически можно изобразить в виде прямой на плоской системе координат.

• Найдем координаты прямых линий для имеющихся уравнений. Уравнение прямой на плоскости строится по двум точкам, каждая из которых имеет две координаты – х1 и х2. Рекомендуется следующее правило построения ограничивающих прямых линий в плоскости координат. Поочередно принимаем, что выпускается только одно из двух изделий, например x_2.  Тогда x₁ полагают равным нулю и определяют значение x₁. Затем, аналогично определяют x₂, принимая x₁ равным нулю.

Например: 0x₁ + 2x₂ = 98705

Для первого ограничения при x₁ = 0 x₂ = = 49352,5;

2x₁ + 0x₂ = 98705.    При x₂ = 0  x₁ = = 49352,5.

Имеем две точки с координатами (0; 49352,5) и (49352,5; 0).

• Строим прямую первого ограничения в системе координат, где на оси ординат ОХ₁ откладываем в принятом масштабе объем производства кронштейнов, на оси ОХ₂ – объем производства валов (см. рисунок).
• Таким же образом строим прямые следующих шести ограничений.
• Найдем область допустимых решений (ОДР). При ограничениях, имеющих знак «меньше или равно», ОДР располагается между осями координат и прямой, отвечает условию данного ограничения. Т.е все точки, лежащие внутри этой области, удовлетворяют соответствующему ограничению.

 

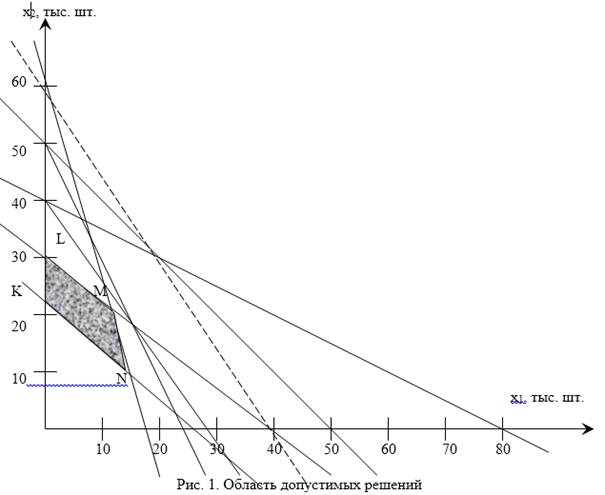
Для последнего, седьмого ограничения ОДР будет находиться выше прямой, описанной этим ограничением, так как знак неравенства – «больше или равно». Оптимальный вариант программы должен располагаться в области, ограниченной всеми семью ограничениями. В нашем случае (рисунок) – это заштрихованная область NKLM. Согласно правилам линейного программирования, экстремальными свойствами обладают только вершины полученного многоугольника.

• Определим значения переменных Xi, соответствующих вершинам многоугольника NKLM, и рассчитаем на их основе значение целевой функции. Определяем графически координаты всех вершин. Вершине L соответствуют x₁ = 0, x₂ = 30000, значение целевой функции равно Z(x) = 6*0+4*30000 = 120000; вершине М соответствуют x₁ = 13000, x₂ = 21000, Z(x) = 6*11000 + 4*21000 = 150000; вершине N соответствуют x₁ = 16000, x₂ =  8000, Z(x) = 6*16000+4*8000 = 128000; вершине К соответствуют x₁ = 0, x₂ = 21000, Z(x) = 4*0+ 6*21000 = 126000.
• Определяем оптимальную программу предприятия по максимальному значению целевой функции.

6. Вывод. Оптимальной является производственная программа выпуска кронштейнов в количестве 13000 шт., валов – 21000 шт., при этом объем НЧП достигает максимального значения – 150000 р.