Билет 1

1) Криволинейный интеграл по длине дуги и его вычисление.

2) Вычислить двойной интеграл , где область D:   х + у = 1,   у = х,   х = 0.

3)Решит уравнение

Билет 2

1) Криволинейные интегралы по координатам и их вычисление.

2) Пользуясь полярными координатами, найти массу пластины D: х² + х² = 16, если плотность ее r = ху,.

3) Решить уравнение

Билет 3

1) Определение двойного интеграла и его основные свойства.

2) Найти аналитическую функцию v  = f (z),  если известно, что u (x,y) = x² – y² и w (0) = 6.

3) Решить уравнение

Билет 4

1) Определение тройного интеграла и его основные свойства.

2) Найти массу кривой y = x³ и 0 £ х £ 2, если плотность ее r  = х².

3) Решить уравнение

Билет 5

1) Поверхностный интеграл по площади поверхности и его основные свойства.

2) Вычислить работу силового поля  вдоль кривой, y = 2x²  от А(0; 0) до В(2; 8).

3)  Решить уравнение

Билет 6

1) Вычисление тройного интеграла в сферических координатах.

2) Найти все особые точки функции 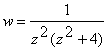 и указать их характер.

3)  Решить уравнение

Билет 7

1) Поверхностные интегралы по координатам и их основные свойства.

2) Изменить порядок интегрирования в .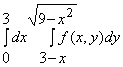

3)  Решить уравнение

Билет 8

1) Показательная функция комплексного переменного и ее связь с тригонометрическими функциями.

2) Пользуясь теоремой Остроградского, найти поток векторного поля  через внешнюю сторону поверхности х² + у² + z² = 4,.

3)  Решить уравнение

Билет 9

1) Логарифмическая функция комплексного переменного. Главное значение логарифма.

2) Найти дивергенцию поля

3)  Решить уравнение

Билет 10

1) Теорема Даламбера-Эйлера.

2) Вычислить (1 + i)ⁱ.

3)  Решить уравнение

Билет 11

1) Теорема Коши для односвязной области.

2) Вычислить циркуляцию векторного поля вдоль указанного замкнутого контура К: 

3)  Решить уравнение

Билет 12

1) Основная теорема Коши о вычетах.

2) Дано векторное поле   Показать, что поле потенциальное и найти потенциал.

3)  Решить уравнение

Билет 13

1) Нахождение функции по полному дифференциалу.

2) Вычислить интеграл  по произвольной линии, соединяющей точки  0 и 5i.

3)  Решить уравнение

Билет 14

1) Разложение функции w = f(z) в ряд Лорана.

2) Найти массу пластины, ограниченной линиями  у = х², у = х,  если r(х, у) = у.

3)  Решить уравнение

Билет 15

1) Ряд Тейлора для функции w = f(z). Нахождение радиуса сходимости.

2) С помощью преобразования к полярным координатам вычислить  если D – круг х² + у² £ 4.

3)  Решить уравнение

Билет 16

1) Вычисление потока векторного поля по теореме Остроградского.

2) Разложить в ряд Тейлора по степеням z функции   е^z   и   sin z.

3)  Решить уравнение

Билет 17

1) Вывести уравнение колебания закрепленной в двух точках струны.

2) Разложить в ряд по степеням   z   функцию w = z³ е^{1/ z}.

3)  Решить уравнение

Билет 18

1) Метод бегущих волн (метод Даламбера) для уравнения бесконечной струны.

2) Вычислить

3)  Решить уравнение

Билет 19

1) Вывод уравнения теплопроводности для конечного стержня.

2) Вычислить

3)  Решить уравнение

Билет 20

1) Постановка задачи для уравнения малых поперечных колебаний закрепленной в двух точках струны.

2) Найти вычеты функции  во всех ее особых точках.

3)  Решить уравнение