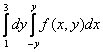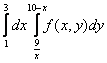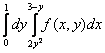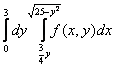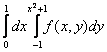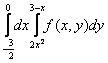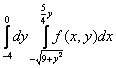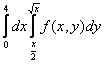Изменить порядок интегрирования в интеграле. Область интегрирования изобразить на рисунке.
|
1) 2) 3) 4) 5) |
6) 7) 8) 9) 10) |
.
Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах.
|
11) 12) 13) 14) 15) |
16) 17) 18) 19) 20) |
.
Дано скалярное поле 
и точка М ее координатами. Найти направление скорости возрастания поля в точке М.
|
21) 22) 23) 24) 25) |
26) 27) 28) 29) 30) |
Найти векторные линии векторного поля.
|
31) 32) 33) 34) 35) |
36) 37) 38) 39) 40) |
Вычислить поток векторного поля 
через треугольник 
, вырезанный из плоскости P координатными плоскостями, в том направлении нормали к плоскости, которое образует осью ох острый угол; а также по формуле Остроградского поток этого же векторного поля через замкнутую поверхность пирамиды, образовавшейся, присоединением к поверхности 
боковых треугольников, которые лежат в координатных плоскостях (нормаль внешняя).
|
41) 42) 43) 44) 45) |
46) 47) 48) 49) 50) |
Вычислить циркуляцию Г поля вектора 
вдоль линии пересечения указанной плоскости (Р) с координатными плоскостями непосредственно и по теореме Стокса. При
этом то направления обхода линии интегрирования считать положительным, при котором точка пробегает ее по ходу часовой стрелки, если смотреть из начала координат.
|
51) 52) 53) 54) 55) |
56) 57) 58) 59) 50) |
Дано векторное поле 
. Требуется узнать: будет ли оно солиноидальным или потенциальным? В случаи потенциальности поля найти его потенциальную функцию 
.
61) 
.
62) 
.
63) 
.
64) 
.
65) 
.
66) 
.
67) 
.
68) 
.
69) 
.
70) 
.
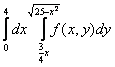